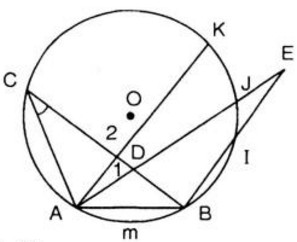
Bài 88 trang 103 SGK Toán 9 tập 2

Hãy nêu tên mỗi góc trong các hình dưới đây:

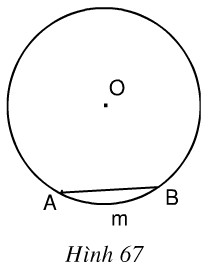
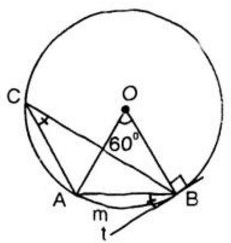
(Ví dụ. góc trên hình 66b) là góc nội tiếp).

Hướng dẫn làm bài:

a) Góc ở tâm.

b) Góc nội tiếp.

c) Góc tạo bởi tiếp tuyến và dây cung.

d) Góc có đỉnh bên trong đường tròn.

e) Góc có đỉnh bên ngoài đường tròn.

Bài 89 trang 104 SGK Toán 9 tập 2

Trong hình 67, cung AmB có số đo là 66^o. Hãy:

a) Vẽ góc ở tâm chắn cung AmB. Tính góc AOB.

b) Vẽ góc nội tiếp đỉnh C chắn cung AmB. Tính góc ACB.

c) Vẽ góc tạo bởi tia tiếp tuyến Bt và dây cung BA. Tính góc ABt.

d) Vẽ góc ADB có đỉnh D ở bên trong đường tròn. So sánh $\widehat{ADB}$  với $\widehat{ACB}$ .

e) Vẽ góc AEB có đỉnh E ở bên ngoài đường tròn (E và C cùng phía đối với AB). So sánh $\widehat{AEB}$ với $\widehat{ACB}$

Hướng dẫn trả lời:

a) Từ O nối với hai đầu mút của cung AB

Ta có $\widehat{AOB}$ là góc ở tâm chắn cung AB

Vì $\widehat{AOB}$ là góc ở tân chắn cung AB nên

$\widehat{AOB}$ = sđ cung AB = 60°

b) Lấy một điểm C bất kì trên (O). Nối C với hai đầu mút của cung AmB. Ta được góc nội tiếp $\widehat{ACB}$

Khi đó: $\widehat{ACB}=\frac{1}{2}sđcungAmB=\frac{1}{2}{60}^0=30$  

c) Vẽ bán kính OB. Qua B vẽ Bt ⊥ OB. Ta được góc Abt là góc tạo bởi tia tiếp tuyến Bt với dây cung BA.

Ta có: $\widehat{ABt}=\frac{1}{2}sđcungAmB={30}^0$

d) Lấy điểm D bất kì ở bên trong đường tròn (O). Nối D với A và D với B. ta được góc  là góc ở bên trong đường tròn (O)

Ta có:  

$\begin{array}{c}\widehat{ACB}=\frac{1}{2}sđcungAmB\\ \widehat{ADB}=\frac{1}{2}\left(sđcungAmB+sđcungCK\right)\end{array}$

Mà sđcung AmB + sđcung CK > sđcung AmB (do sđcung CK > 0) nên $\widehat{ADB}>\widehat{ACB}$  

e) Lấy điểm E bất kì ở bên ngoài đường tròn, nối E với A và E với B, chúng cắt đường tròn lần lượt tại J và I.

Ta có góc AEB là góc ở bên ngoài đường tròn (O)

Có:

$\begin{array}{c}\widehat{ACB}=\frac{1}{2}sđcungAmB\\ \widehat{AEB}=\frac{1}{2}\left(sđcungAmB-sđcungIJ\right)\end{array}$

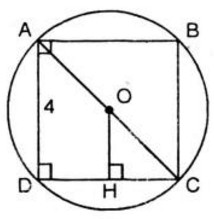
Mà sđcung AmB – sđ cung IJ < sđcung AmB (do sđcung IJ > 0)

Nên $\widehat{AEB}<\widehat{ACB}$ 

Bài 90 trang 104 SGK Toán 9 tập 2

a) Vẽ hình vuông cạnh 4cm.

b) Vẽ đường tròn ngoại tiếp hình vuông đó. Tính bán kính R của đường tròn này.

c) Vẽ đường tròn nội tiếp hình vuông đó. Tính bán kính r của đường tròn này.

Hướng dẫn trả lời:

a) Dùng êke ta vẽ hình vuông ABCD có cạnh bằng 4cm như sau:

- Vẽ AB = 4cm.

- Vẽ BC  ⊥ AB và BC = 4cm

- Vẽ DC ⊥ BC và DC = 4cm

- Nối D với A, ta có AD ⊥ DC và AD = 4cm

b) Tam giác ABC là tam giác vuông cân nên AB = BC.

Áp dụng định lí Py – ta – go trong tam giác vuông ABC, ta có:

$\begin{array}{c}A{C}^2=A{B}^2+B{C}^2=2A{B}^2\iff A{C}^2={2.4}^2=32\\ \Rightarrow AC=\sqrt{32}=4\sqrt{2}\end{array}$

Vậy $AO=R=\frac{AC}{2}=\frac{4\sqrt{2}}{2}=2\sqrt{2}$ 

Vậy R  = 2√2 cm

c) Vẽ OH ⊥ Dc. Vẽ đường tròn tâm O, bán kính OH. Đó là đường tròn nội tiếp hình vuông ABCD

Ta có: $OH=\frac{AD}{2}=2\left(cm\right)$  

Vậy r = OH = 2cm

Bài 91 trang 104 SGK Toán 9 tập 2

Trong hình 68, đường tròn tâm O có bán kính R = 2cm, góc AOB = 75^o.

a) Tính sđ cung ApB.

b) Tính độ dài hai cung AqB và ApB.

c) Tính diện tích hình quạt tròn OaqB

Hướng dẫn trả lời:

a) Ta có $\widehat{AOB}$ là góc nội tiếp chắn cung AqB nên:

$\widehat{AOB}$ = sđcung AqB hay sđcung AqB = 75°

Vậy sđ cungApB = 360°- sđcung AqB = 360° - 75° = 285°

b) $l_{cungAqB}$ là độ dài cung AqB, ta có:

$l_{cungAqB}=\frac{\pi Rn}{180}=\frac{\pi .2.75}{180}=\frac{5}{6}\pi \left(cm\right)$ 

Gọi $l_{cungApB}$ là độ dài cung ApB ta có:

$l_{cungApB}=\frac{\pi Rn}{180}=\frac{\pi .2.285}{180}=\frac{19\pi }{6}\left(cm\right)$

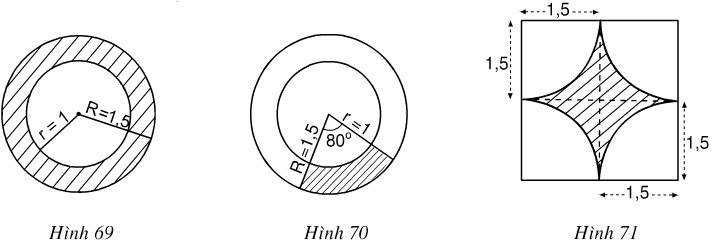
c) Diện tích hình quạt tròn OaqB là:  $S_{OAqB}=\frac{\pi R^{2}n}{360}=\frac{\pi 2^{2}75}{350}=\frac{5\pi }{6}\left(c{m}^2\right)$

Bài 92 trang 104 SGK Toán 9 tập 2

Hãy tính diện tích miền gạch sọc trong các hình 69, 70, 71 (đơn vị độ dài: cm).

Hướng dẫn trả lời:

a) Hình 69

Đối với hình tròn bán kính R = 1,5: S₁ = πR² = π. 1,5² = 2,25π

Đối với hình tròn bán kính r = 1: S₂ = πr² = π. 1² = π

Vậy diện tích miền gạch sọc là:

S = S₁ – S­₂ = 2,25 π – π = 1,25 π (đvdt)

b) Hình 70

Diện tích hình quạt có bán kính R = 1,5; n° = 80°

$S_1=\frac{\pi R^{2}n}{360}=\frac{\pi 1,5^2.80}{360}=\frac{\pi }{2}$ 

Diện tích hình quạt có bán kính r = 1; n° = 80°

$S_2=\frac{\pi r^{2}n}{360}=\frac{\pi {.1}^2.80}{360}=\frac{2\pi }{9}$

Vậy diện tích miền gạch sọc là: $S=S_1-S_2=\frac{\pi }{2}-\frac{2\pi }{9}=\frac{9\pi -4\pi }{18}=\frac{5\pi }{18}$

c) Hình 71

Diện tích hình vuông cạnh a = 3 là:

S₁ = a² = 3² =9

Diện tích hình tròn có R = 1,5 là:

S₂ = πR² = π.1,5 ² = 2,25π = 7,06

Vậy diện tích miền gạch sọc là:

S = S₁ – S₂ = 9 – 7,06 = 1,94 (đvdt).