Bài 77 trang 98 sgk toán lớp 9 tập 2

Tính diện tích hình tròn nội tiếp một hình vuông cạnh là 4cm.

Hướng dẫn giải:

Hình tròn nội tiếp một hình vuông cạnh là 4cm thì có bán kính là 2cm. 

Vậy diện tích hình tròn là π(2²) = 4π (cm²)

Bài 78 trang 98 sgk toán lớp 9 tập 2

Chân một đống cát trên một nền phẳng nằm ngang là một hình tròn có chu vi là 12 m. Hỏi chân đống cát đó chiếm một diện tích bao nhiêu mét vuông?

Hướng dẫn giải:

Theo giả thiết thì C = 2πR = 12m => R = $\frac{12}{2\pi }$ = $\frac{6}{\pi }$.

Diện tích phần mặt đất mà đống cát chiếm chỗ là:

            S = π. R² = π ${\left(\frac{6}{\pi }\right)}^2$ = $\frac{36}{\pi }$ ≈ 11,5 (m²)

Bài 79 trang 98 sgk toán lớp 9 tập 2

Tính diện tích một hình quạt tròn có bán kính 6cm, số đo cung là 36^o  

Hướng dẫn giải:

Theo công thức S = $\frac{\pi R^2{n}^{\circ }}{{360}^{\circ }}$ ta có S= $\frac{\pi 6^2.36}{360}$ ≈ 3,6π (cm²)

Bài 80 trang 98 sgk toán lớp 9 tập 2

Một vườn cỏ hình chữ nhật ABCD có AB = 40m, AD = 30m

Người ta muốn buộc hai con dê ở hai góc vườn A, B. Có hai cách buộc:

- Mỗi dây thừng dài 20m.

- Một dây thừng dài 30m và dây thừng kia dài 10m.

Hỏi cách buộc nào thì diện tích cỏ mà cả hai con dê có thể ăn được sẽ lớn hơn (h.60)

Hướng dẫn giải:

Theo cách buộc thứ nhất thì diện tích cỏ dành cho mỗi con dê là bằng nhau.

Mỗi diện tích là $\frac{1}{4}$ hình tròn bán kính 20m.

                    $\frac{1}{4}$ π.20² = 100π (m²)

Cả hai diện tích là 200π (m²)                  (1)

Theo cách buộc thứ hai, thì diện tích cỏ dành cho con dê buộc ở A là 

                  $\frac{1}{4}$ π.30² = $\frac{1}{4}$ 900π (m²)

Diện tích cỏ dành cho con dê buộc ở B là: $\frac{1}{4}$ π.10² = $\frac{1}{4}$ 100π  (m²)

Diện tích cỏ dành cho cả hai con dê là:

                 $\frac{1}{4}$ 900π  + $\frac{1}{4}$ 100π = $\frac{1}{4}$ 1000π = 250π (m²)                   (2)

So sánh (1) và (2) ta thấy với cách buộc thứ hai thì diện tích cỏ mà hai con dê có thể ăn được sẽ lớn hơn.

Bài 81 trang 99 sgk toán lớp 9 tập 2

Diện tích hình tròn sẽ thay đổi như thế nào nếu:

a) Bán kính tăng gấp đôi?

b) Bám kinh tăng gấp ba?

c) Bán kính tăng k lần (k>1)?

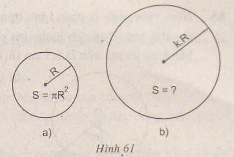
Hướng dẫn giải:

Ta có: 

π(2R)² = 4πR²

π(3R)² = 9 πR²

π(kR)² = k² πR²

 

Vậy nếu ta gấp đôi bán kính thì diện tích hình tròn sẽ gấp bốn, nếu nhân bán kính với k > 0 thì diện tích hình tròn sẽ gấp k² lần.

Bài 82 trang 99 sgk toán lớp 9 tập 2

Điền vào ô trống trong bảng sau (làm tròn kết quả đến chữ số thập phân thứ nhât)

Hướng dẫn giải:

- Dòng thứ nhất: R = $\frac{C}{2\pi }$ = $\frac{13,2}{2.3,14}$ ≈ 2,1 (cm)

                       S = π. R² = 3,14(2,1)² ≈ 13,8 (cm²)

                       R_quạt = $\frac{\pi R^2{n}^{\circ }}{{360}^{\circ }}$ = $\frac{3,14.2,1^2.47,5}{360}$ ≈ 1,83  (cm²)

- Dòng thứ hai: C = 2πR = 2. 3,14. 2,5 = 15,7 (cm)

                       S = π. R² = 3,14(2,5)²  ≈ 19,6 (cm²)

                       n^o = $\frac{S_{quat}{.360}^{\circ }}{\pi R^2}$ = $\frac{12,{5.360}^{\circ }}{3,14.2,5^2}$ ≈ 229,3^o  

- Dòng thứ ba: R = $\sqrt{\frac{s}{\pi }}$ = $\sqrt{\frac{37,8}{3,14}}$ ≈ 3,5 (cm)

                     C = 2πR = 22 (cm)

                      n^o = $\frac{S_{quat}{.360}^{\circ }}{\pi R^2}$= $\frac{10,{6.360}^{\circ }}{3,14.3,5^2}$ ≈ 99,2^o  

Điền vào các ô trống ta được các bảng sau:

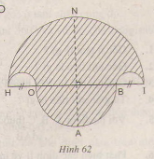
Bài 83 trang 99 sgk toán lớp 9 tập 2

a) Vẽ hình 62 (tạo bởi các cung tròn) với HI = 10cm và HO = 2cm. Nêu cách vẽ.

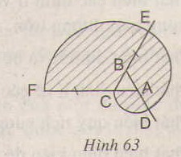
b) Tính diện tích hình HOABINH (miền gạch sọc)

c) Chứng tỏ rằng hình tròn đường kính NA có cùng diện tích với hình HOABINH đó.

Hướng dẫn giải:

a) Vẽ nửa đường tròn đường kính HI = 10 cm, tâm M

Trên đường kính HI lấy điểm O và điểm B sao cho HO = BI = 2cm.

Vẽ hai nửa đường tròn đường kính HO, BI nằm cùng phía với đường tròn (M).

vẽ nửa đường tròn đường kính OB nằm khác phía đối với đường tròn (M). Đường thẳng vuông góc với HI tại M cắt (M) tại N và cắt đường tròn đường kính OB tại A.

b)  Diện tích hình HOABINH là:

$\frac{1}{2}$.π 5² + $\frac{1}{2}$.π.3² – π.1² = $\frac{25}{2}$π + $\frac{9}{2}$π - π = 16π (cm²)        (1)

c) Diện tích hình tròn đường kính NA bằng:

             π. 4² = 16π  (cm²)                                           (2)

So sánh (1) và (2) ta thấy hình tròn okính NA có cùng diện tích với hình HOABINH

Bài 84 trang 99 sgk toán lớp 9 tập 2

a) Vẽ lại hình tạo bởi các cung tròn xuất phát từ đỉnh C của tam giác đều ABC cạnh 1 cm. Nêu cách vẽ (h.63).

b) Tính diện tích miền gạch sọc.

Hướng dẫn giải:

a) Vẽ tam giác đều ABC cạnh 1cm

Vẽ $\frac{1}{3}$ đường tròn tâm A, bán kính 1cm, ta được cung 

Vẽ $\frac{1}{3}$ đường tròn tâm B, bán kính 2cm, ta được cung 

Vẽ $\frac{1}{3}$ đường tròn tâm C, bán kính 3cm, ta được cung 

b) Diện tích hình quạt CAD = $\frac{1}{3}$ π.1²

Diện tích hình quạt DBE = $\frac{1}{3}$ π.2² 

 

Diện tích hình quạt ECF = $\frac{1}{3}$ π.3²

Diện tích phần gạch sọc =  $\frac{1}{3}$ π.1²+ $\frac{1}{3}$ π.2² + $\frac{1}{3}$ π.3²

                                   = $\frac{1}{3}$ π (1² + 2² + 3²) = $\frac{14}{3}$π (cm²)

Bài 85 trang 100 sgk toán lớp 9 tập 2

Hình viên phân là hình tròn giới hạn bởi một cung tròn và dây căng cung ấy. Hãy tính diện tích hình viên phân AmB, biết góc ở tâm 

$\widehat{AOB}={60}^0$ và bán kính đường tròn là 5,1 cm (h.64)

Hướng dẫn giải:

∆OAB là tam giác đều có cạnh bằng R = 5,1cm. Áp dụng công thức tính diện tích tam giác đều cạnh a là $\frac{a^2\sqrt{4}}{4}$ ta có 

S_∆OBC = $S_{\Delta OBC}=\frac{R^2\sqrt{3}}{4}$           (1)

Diện tích hình quạt tròn AOB là:

 $\frac{\pi .R^2{.60}^0}{{360}^0}=\frac{\pi R^2}{6}$     (2)

Từ (1) và (2) suy ra diện tích hình viên phân là:

$\frac{\pi R^2}{6}-\frac{R^2\sqrt{3}}{4}=R^2\left(\frac{\pi }{6}-\frac{\sqrt{3}}{4}\right)$

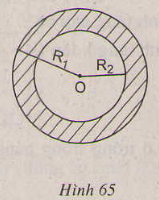
Thay R = 5,1 ta có S_{viên phân} ≈ 2,4 (cm²)

Bài 86 trang 100 sgk toán lớp 9 tập 2

Hình vành khăn là phần hình tròn nằm giữa hai đường tròn đồng tâm (h.65).

a) Tính diện tích S của hình vành khăn theo R₁ và R₂ (giả sử R₁ > R₂).

b) Tính diện tích hình vành khăn khi R₁ = 10,5 cm, R₂ = 7,8 cm.

Hướng dẫn giải:

a) Diện tích hình tròn (O;R₁) là S₁ = πR₁².

Diện tích hình tròn (O;R₂) là S₂ = πR₂².

Diện tích hình vành khăn là:

       S = S₁ – S₂ = πR₁²- πR₂² = π( R₁² – R₂²)

b) Thay số: S = 3,14. (10,5² – 7,8²) = 155,1(cm²)

Bài 87 trang 100 sgk toán lớp 9 tập 2

Lấy cạnh BC của một tam giác đều làm đường kính, vẽ một nửa đường tròn về cùng một phía với tam giác ấy đối với đường thẳng BC. Cho biết cạnh BC = a, hãy diện tích hình viên phân được tạo thành.

Hướng dẫn giải:

Gọi nửa đường tròn tâm O đường kính BC căt hai cạnh AB và AC lần lượt tại M và N.

∆ONC có OC = ON, $\hat{C}$ = 60^o nên ∆ONC là tam giác đều, do đó $\widehat{NOC}$ = 60^o.

S_{quạt NOC} = $\frac{\pi {\left(\frac{a}{2}\right)}^2{.60}^{\circ }}{{360}^{\circ }}$ = $\frac{\pi a^2}{24}$.

S_∆NOC = $\frac{{\left(\frac{a}{2}\right)}^2\sqrt{3}}{4}$ = $\frac{a^2\sqrt{3}}{16}$

Diện tích hình viên phân: 

S_CpN  = $\frac{\pi a^2}{24}$ - $\frac{a^2\sqrt{3}}{16}$ = $\frac{a^2}{48}\left(2\pi -3\sqrt{3}\right)$

Vậy diện tích hình viên phhân bên ngoài tam giác là:

            $\frac{a^2}{24}\left(2\pi -3\sqrt{3}\right)$