|
||||||||||||||
|
|
||||||||||||||
|
Tìm kiếm
Danh mục
Hàng mới
 Phần mềm trình chiếu Powerpoint 400.000 VNĐ  Trợ giúp trình chiếu Powerpoint 50.000 VNĐ  Nhận gia công website 999.000 VNĐ
Liên hệ: Minh
0976.775.168
Quảng cáo
|
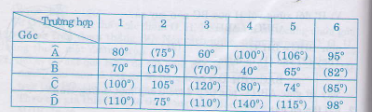
Bài 53 trang 89 sgk toán lớp 9 tập 2 Biết ABCD là tứ giác nội tiếp. Hãy điền vào ô trống trong bẳng sau (nếu có thể)
Hướng dẫn giải: - Trường hợp 1: Ta có + = 180o => = 180o - = 180o – 80o = 100o + = 180o => = 180o - = 180o – 70o = 110o Vậy điểm = 100o , = 110o - Trường hợp 2: Ta có + = 180o => = 180o - = 180o – 105o = 75o + = 180o => = 180o - = 180o – 75o = 105o - Trường hợp 3: + = 180o => = 180o - = 180o – 60o = 120o + = 180o Chẳng hạn chọn = 70o , = 110o - Trường hợp 4: = 180o - = 180o – 40o = 140o Còn lại + = 180o Chẳng hạn chọn = 100o , = 80o - Trường hợp 5: = 180o - = 180o – 74o = 106o = 180o - = 180o – 65o = 115o - Trường hợp 6: = 180o - = 180o – 95o = 85o = 180o - =180o – 98o = 82o Vậy điền vào ô trống ta được bảng sau:
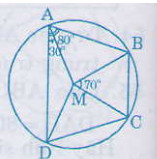
Bài 54 trang 89 sgk toán lớp 9 tập 2 Tứ giác ABCD có + = 180o. Chứng minh rằng các đường trung trực của AC, BD, AB cùng đi qua một điểm. Hướng dẫn giải: Tứ giác ABCD có tổng hai góc đối diện bằng 180o nên nội tiếp đường tròn tâm O, ta có OA = OB = OC = OD Do đó các đường trung trực của AB, BD, AB cùng đi qua O Bài 55 trang 89 sgk toán lớp 9 tập 2 Cho ABCD là một tứ giác nội tiếp đường tròn tâm M, biết 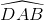 = 80o, = 80o, 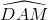 = 30o, = 30o, 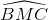 = 70o. = 70o.
Hãy tính số đo các góc Hướng dẫn giải:
Ta có: - ∆MBC là tam giác cân (MB= MC) nên - ∆MAB là tam giác cân (MA=MB) nên Vậy
=> sđ cung BCD = 2 Mà sđ cung BC = Vậy cung DC = 160o – 70o = 90o (vì C nằm trên cung nhỏ cung BD) Suy ra ∆MAD là tam giác cân (MA= MD) Suy ra ∆MCD là tam giác vuông cân (MC= MD) và Suy ra
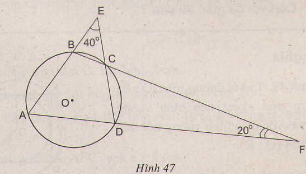
Bài 56 trang 89 sgk toán lớp 9 tập 2 Xem hình 47. Hãy tìm số đo các góc của tứ giác ABCD
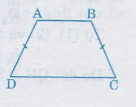
Hướng dẫn giải: Ta có = (hai góc đối đỉnh) Đặt x = = . Theo tính chất góc ngoài tam giác, ta có: = x + 40o (1) = x +20o (2) Lại có + = 180o (3) (hai góc đối diện tứ giác nội tiếp) Từ (1), (2), (3) suy ra: 180o = 2x + 60o => x = 60o Từ (1), ta có: = 60o + 40o = 100o Từ (2), ta có: = 60o + 20o = 80o = 180o – x (hai góc kề bù) => = 120o = 180o - (hai góc đối diện của tứ giác nội tiếp) => = 180o – 120o = 60o Bài 57 trang 89 sgk toán lớp 9 tập 2 Trong các hình sau, hình nào nội tiếp được một đường tròn: Hình bình hành, hình chữ nhật, hình vuông, hình thang, hình thang vuông, hình thang cân ? Vì sao? Hướng dẫn giải: Hình bình hành nói chung không nội tiếp được đường tròn vì tổng hai góc đối diện không bằng 180o.Trường hợp riêng của hình bình hành là hình chữ nhật (hay hình vuông) thì nội tiếp đường tròn vì tổng hai góc đối diện là 90o + 90o = 180o
Hình thang nói chung, hình thang vuông không nội tiếp được đường tròn. Hình thang cân ABCD (BC= AD) có hai góc ở mỗi đáy bằng nhau = , = ; mà + = 180o (hai góc trong cùng phía tạo bởi cát tuyến AD với AD // CD),suy ra + = 180o . Vậy hình thang cân luôn có tổng hai góc đối diện bằng 180o nên nội tiếp được đường tròn Bài 58 trang 90 sgk toán lớp 9 tập 2 Cho tam giác đều ABC. Trên nửa mặt phẳng bờ BC không chứa đỉnh A, lấy điểm D sao cho DB = DC và = . a) Chứng minh ABDC là tứ giác nội tiếp. b) Xác định tâm của đường tròn đi qua bốn điểm A, B, D, C. Hướng dẫn giải: a) Theo giả thiết, = = .60o = 30o = + (tia CB nằm giữa hai tia CA, CD) => = 60o + 30o = 90o (1) Do DB = CD nên ∆BDC cân => = = 30o Từ đó = 60o + 30o = 90o (2) Từ (1) và (2) có + = 180o nên tứ giác ABDC nội tiếp được. b) Vì = 90o nên AD là đường kính của đường tròn ngoại tiếp tứ giác ABDC, do đó tâm đường tròn ngoại tiếp tứ giác ABDC là trung điểm AD.
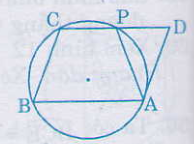
Bài 59 trang 90 sgk toán lớp 9 tập 2 Cho hình bình hành ABCD. Đường tròn đi qua ba đỉnh A, B, C cắt đường thẳng CD tại P khác C. Chứng minh AP = AD Hướng dẫn giải: Do tứ giác ABCP nội tiếp nên ta có: + = 180o (1) Ta lại có: + = 180o (2) (hai góc trong cùng phía tạo bởi cát tuyến CB và AB // CD) Từ (1) và (2) suy ra: = Vậy ABCP là hình thang cân, suy ra AP = BC (3) nhưng BC = AD (hai cạnh đối đỉnh của hình bình hành) (4) Từ (3) và (4) suy ra AP = AD.
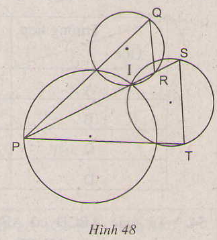
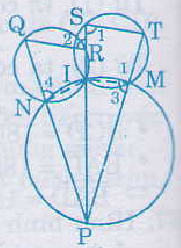
Bài 60 trang 90 sgk toán lớp 9 tập 2 Xem hình 48. Chứng minh QR // ST.
Hướng dẫn giải: Kí hiệu như hình vẽ.
Ta có tứ giác ISTM nội tiếp đường tròn nên: + = 180o Mà + = 180o (kề bù) nên suy ra = (1) Tương tự từ các tứ giác nội tiếp IMPN và INQS ta được = (2) = (3) Từ (1), (2), (3) suy ra Do đó QR // ST |
Đăng nhập
Giỏ hàng
Hàng bán chạy
 Phần mềm Quản lý kho Offline 299.000 VNĐ  Monkey Stories 499.000 VNĐ  Monkey Math 499.000 VNĐ
Thống kê
Lượt truy cập : 940329
Số người online : 128 + Khách : 128 + Thành viên : 0
Quảng cáo
|
||||||||||||
| Trang chủGiới thiệuSản phẩmInsight EnglishBHXHDatabaseTiện íchGiải tríKhoảng trờiWall Web | ||||||||||||||
|
||||||||||||||







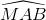 ,
, 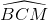 ,
, 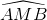 ,
, 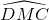 ,
, 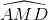 ,
, 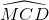 và
và 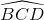 .
.
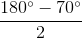 = 55o (2)
= 55o (2)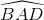 =
=  sđcung BCD (số đo góc nội tiếp bằng nửa số đo của cung bị chắn)
sđcung BCD (số đo góc nội tiếp bằng nửa số đo của cung bị chắn)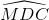 = 45o (6)
= 45o (6)