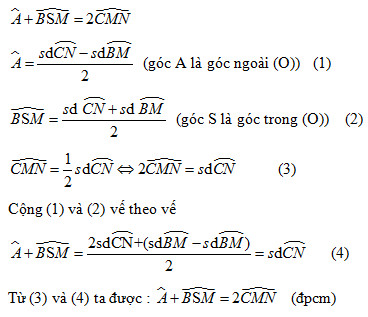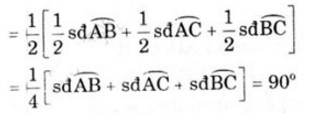|
||||||||||||||
|
|
||||||||||||||
|
Tìm kiếm
Danh mục
Hàng mới
 Phần mềm trình chiếu Powerpoint 400.000 VNĐ  Trợ giúp trình chiếu Powerpoint 50.000 VNĐ  Nhận gia công website 999.000 VNĐ
Liên hệ: Minh
0976.775.168
Quảng cáo
|
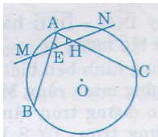
Bài 36 trang 82 sgk toán lớp 9 tập 2 Cho đường tròn (O) và hai dây AB, AC. Gọi M, N lần lượt là điểm chính giữa của cung AB và cung AC. Đường thẳng MN cắt dây AB tại E và cắt dây AC tại H. Chứng minh rằng tam giác AEH là tam giác cân. Hướng dẫn giải:
Ta có:
(Vì Theo gỉả thiết thì: Từ (1),(2), (3), (4), suy ra Bài 37 trang 82 sgk toán lớp 9 tập 2 Cho đường tròn (O) và hai dây AB, AC bằng nhau. Trên cung nhỏ AC lấy một điểm M. Gọi S là giao điểm của AM và BC. Chứng minh 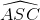 = = 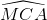 . .
Hướng dẫn giải:
Ta có: ( và (góc nội tiếp chắn cung Theo giả thiết thì: AB = AC => Từ (1), (2), (3) suy ra:
Từ đó Bài 38 trang 82 sgk toán lớp 9 tập 2 Trên một đường tròn, lấy liên tiếp ba cung AC, CD, DB sao cho sđ cung AC = sđ cung CD = sđ cung DB = 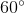 . Hai đường thẳng AC và BD cắt nhau tại E. Hai tiếp tuyến của đường tròn tại B và C cắt nhau tại T. Chứng minh rằng: . Hai đường thẳng AC và BD cắt nhau tại E. Hai tiếp tuyến của đường tròn tại B và C cắt nhau tại T. Chứng minh rằng:
a) b) CD là phân giác của Hướng dẫn giải: a) Ta có
và
Vậy b)
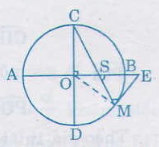
Vậy Bài 39 trang 83 sgk toán lớp 9 tập 2 Cho AB và CD là hai đường kính vuông góc của đường tròn (O). Trên cung nhỏ BD lấy một điểm M. Tiếp tuyến tại M cắt tia AB ở E, đoạn thẳng CM cắt AB ở S.Chứng minh ES = EM. Hướng dẫn giải: Ta có = ( vì là góc có đỉnh S ở trong đường tròn (O)) = ( là góc tạo bởi tiếp tuyến và dây cung). Theo giả thiết Từ (1), (2), (3) ta có: = từ đó ∆ESM là tam giác cân và ES = EM
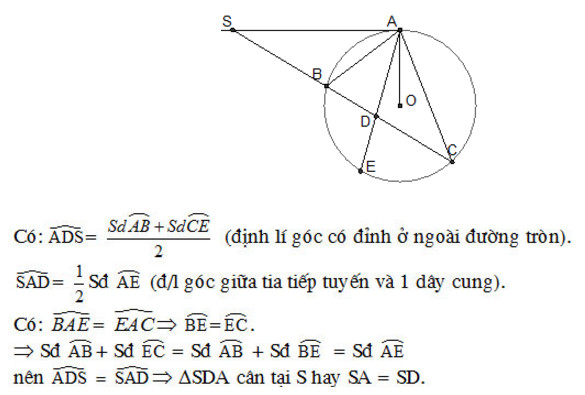
Bài 40 trang 83 sgk toán lớp 9 tập 2 Qua điểm S nằm bên ngoài đường tròn (O), vẽ tiếp tuyến SA và cát tuyến SBC của đường tròn. Tia phân giác của góc BAC cắt dây BC tại D. Chứng minh SA = SD Trả lời:
Bài 41 trang 83 sgk toán lớp 9 tập 2 Qua điểm A nằm bên ngoài đường tròn (O) vẽ hai cát tuyến ABC và AMN sao cho hai đường thẳng BN và CM cắt nhau tại một điểm S nằm bên trong đường tròn. Chứng minh:
Hướng dẫn giải:
Ta có :
Cho tam giác ABC nội tiếp đường tròn. P, Q, R theo thứ tự là các điểm chính giữa các cung bị chắn BC, CA, AB bởi các góc A, B, C. a) Chứng minh AP ⊥ QR b) AP cắt CR tại I. Chứng minh tam giác CPI là tam giác cân Hướng dẫn giải: a) Gọi giao điểm của AP và QR là K. ∠AKR là góc có đỉnh ở bên trong đường tròn nên ∠AKR = sđcung(AR +QC + CP)/2 =
Vậy ∠AKR = 900 hay AP ⊥ QR b) ∠CIP là góc có đỉnh ở bên trong đường tròn nên: ∠CIP = sđcung(AR +CP)/2 (1) ∠PCI góc nội tiếp, nên ∠PCI= (sđ cung RB + BP)/2 (2) Theo giả thiết thì cung AR = RB (3) Cung CP = BP (4) Từ (1), (2), (3), (4) suy ra: ∠CIP = ∠PCI. Do đó ∆CPI cân. Bài 43 trang 83 sgk toán lớp 9 tập 2 Cho đường tròn (O) và hai dây cung song song AB, CD (A và C nằm trong cùng một nửa mặt phẳng bờ BD); AD cắt BC tại I Chứng minh = . Hướng dẫn giải:
Theo giả thiết: = Theo (1) suy ra = sđ = sđ So sánh (3), (4), ta có = . |
Đăng nhập
Giỏ hàng
Hàng bán chạy
 Phần mềm Quản lý kho Offline 299.000 VNĐ  Monkey Stories 499.000 VNĐ  Monkey Math 499.000 VNĐ
Thống kê
Lượt truy cập : 939764
Số người online : 30 + Khách : 30 + Thành viên : 0
Quảng cáo
|
||||||||||||
| Trang chủGiới thiệuSản phẩmInsight EnglishBHXHDatabaseTiện íchGiải tríKhoảng trờiWall Web | ||||||||||||||
|
||||||||||||||






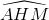 =
=  (1)
(1)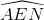 =
= 

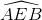 =
= 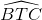 ;
;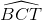
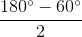 =
= 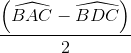 =
= 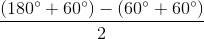 =60
=60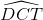 là góc tạo bởi tiếp tuyến và dây cung nên:
là góc tạo bởi tiếp tuyến và dây cung nên: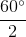 =
= 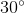
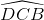 là góc nội tiếp trên
là góc nội tiếp trên