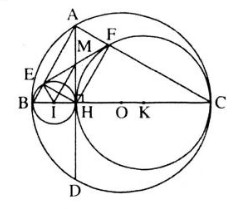
Bài 41 trang 128 SGK Toán 9 tập 1

Cho đường tròn (O) có đường kính BC, dây AD vuông góc với BC tại H.

Gọi E, F theo thứ tự là chân các đường vuông góc kẻ từ H đến AB, AC. Gọi (I), (K) theo thứ tự là các đường tròn ngoại tiếp tam giác HBE, HCF.

a) Hãy xác định vị trí tương đối của các đường tròn: (I) và (O); (K) và(O); (I) và (K).

b) Tứ giác AEHF là hình gì? Vì sao?

c) Chứng minh đẳng thức AE.AB = AF.AC

d) Chứng minh rằng EF là tiếp tuyến chung của hai đường trong (I) và (K)

e) Xác định vị trí của điểm H để EF có độ dài lớn nhất.

Hướng dẫn làm bài:

a) OI = OB – IB nên (I) tiếp xúc trong với (O)

OK = OC – KC nên (K) tiêó xúc trong với (O)

IK = IH + KH nên (I) tiếp xúc ngoài với (K)

b) Góc BEH = 90° (E thuộc đường tròn đường kính BH)

$\Rightarrow \widehat{AEH}={90}^0$

Tương tự có $\widehat{AFH}={90}^0;\widehat{BAC}={90}^0$

Tứ giác AEHF có $\widehat{EAF}=\widehat{AEH}=\widehat{AFH}={90}^0$ nên là hình chữ nhật.

c) ∆ABH vuông tại H, HE là đường cao nên AH² = AE. AB

∆ACH vuông tại H, HF là đường cao nên AH² = AF. AC

Do đó AE. AB = AF. AC

d) Gọi M là giao điểm của AH và EF, ta có: ME = MF = MH = MA

Xét ∆MEI và ∆MHI có:

ME = MH, IE = IH (=R), MI (cạnh chung)

Do đó ∆MEI = ∆MHI (c.c.c)

$\Rightarrow \widehat{MEI}=\widehat{MHI}$ 

mà $\widehat{MHI}={90}^0$ nên $\widehat{MEI}={90}^0$ 

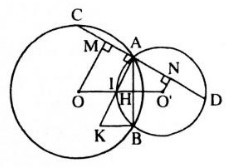
⇒ EF là tiếp tuyến của đường tròn (I)

Chứng minh tương tự có EF là tiếp tuyến của đường tròn (K)

e) Ta có EF = AH mà AH ≤ AO = R

Do đó EF ≤ R, không đổi. Dấu “=” xảy ra ⇔ H ≡ O

Vậy khi dây AD vuông góc với BC tại O thì EF có độ dài lớn nhất

Bài 42 trang 128 SGK Toán 9 tập 1

a) Tứ giác AEMF là hình chữ nhật.

b) ME.MO = MF.MO’

c) OO’ là tiếp tuyến của đường tròn có đường kính là BC.

d) BC là tiếp tuyến của đường tròn có đường kính là OO’.

Hướng dẫn làm bài:

a) MA, MB là các tiếp tuyến của đường tròn (O) (gt).

Theo tính chất của hai tiếp tuyến cắt nhau, ta có MA = MB, MO là tia phân giác góc AMB.

∆MAB cân tại M (MA = MB)

Có MO là đường phân giác nên đồng thời là đường cao

$\Rightarrow MO\perp AB\Rightarrow \widehat{MEA}={90}^0$

Chứng minh tương tự có MO’ là tia phân giác góc AMC và góc MFA = 90°

MO, MO’ là tia phân giác của hai góc kẻ bù $\widehat{AMB},\widehat{AMC}\Rightarrow \widehat{EMF}={90}^0$ 

Tứ giác AEMF là hình chữ nhật (vì $\widehat{EMF}=\widehat{MEA}=\widehat{MFA}={90}^0$  

b) ∆MAO vuông tại A có AE là đường cao nên ME. MO = MA²

Tương tự, ta có: MF. MO’ = MA²

Do ddos, ME. MO = MF. MO’ (= MA²)

c) Ta có MA = MB = MC nên M là tâm đường tròn đường kính BC có bán kính là MA. Mà OO’ ⊥ MA tại A.

Do đó OO’ là tiếp tuyến của đường tròn đường kính BC

d) Gọi K là trung điểm OO’, ta có K là tâm đường tròn có đướng kính là OO’, bán kính KM (∆MOO’ vuông tại M)

Ta có OB ⊥ BC, O’C ⊥ BC ⇒ OB // OC.

Tứ giác OBCO’ là hình thang có K, M lần lượt là trung điểm các cạnh cạnh bên OO’, BC.

Do đó KM là đường trung bình của hình thang OBCO’ ⇒ KM // OB

Mà OB ⊥ BC nên KM ⊥ BC

Ta có BC ⊥ KM tại M nên BC là tiếp tuyến của đường tròn đường kính OO’

Bài 43 trang 128 SGK Toán 9 tập 1

Cho hai đường tròn(O; R) và (O’; r) cắt nhau tại A và B (R > r). Gọi I là trung điểm của OO’. Kẻ đường thẳng vuông góc với IA tại A, đường thẳng này cắt cá đường tròn tâm (O; R) và (O’; r) theo thứ tự tại C và D (khác A).

a) Chứng minh rằng AC = AD.

b) Gọi K là điểm đối xứng với điểm A qua điểm I. Chứng minh rằng KB vuông góc với AB

Hướng dẫn làm bài:

a) Vẽ OM ⊥ CD tại M, O’N ⊥CD tại N, ta có:

 $MA=MC=\frac{AC}{2};$

 $NA=ND=\frac{AD}{2}$

Mặt khác, ta có OM ⊥ CD, IA ⊥ CD, O’N ⊥ CD

⇒ OM // IA //O’N.

Hình thang OMNO’ (OM //O’N) có IA // OM; IO = IO’ nên MA  = NA. Do vậy AC = AD

b) (O) và (O’) cắt nhau tại A, B

⇒ OO’ là đường trung trực của đoạn thẳng AB

⇒ IA = IB

Mặt khác IA = IK ( vì K đối xứng với A qua I)

Do đó: IA = IB = IK

Ta có ∆KBA có BI là đường trung tuyến và $BI=\frac{AK}{2}$ nên ∆KBA vuông tại B

⇒ KB ⊥ AB