a) HB=HC;

b) $\widehat{BAH}$=$\widehat{CAH}$

Giải:

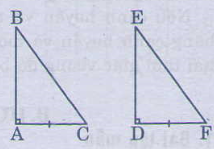
a) Hai tam giác vuông ABH và ACH có: 

AB=AC(gt)

AH cạnh chung.

Nên ∆ABH=∆ACH(Cạnh huyền-cạnh góc vuông)

Suy ra HB=HC

b)∆ABH=∆ACH(Câu a)

Suy ra $\widehat{BAH}$=$\widehat{CAH}$(Hai góc tương ứng)

$\hat{A}$=$\hat{D}$=90⁰, AC=DF. Hãy bổ sung thêm một điều kiện bằng nhau để ∆ABC=∆DEF.

Giải:

Xem hình vẽ

* Bổ sung thêm AB=DE

Thì ∆ABC=∆DEF (c.g.c)

* Bổ sung thêm $\hat{C}$=$\hat{F}$ 

Thì ∆ABC=∆DEF(g.c.g)

* Bổ sung thêm BC=EF

thì ∆ABC=∆DEF (cạnh huyền- cạnh góc vuông)

$\hat{A}$<90⁰). Vẽ BH ⊥ A (H thuộc AC), CK⊥ AB (K thuộc AB)

a) Chứng minh rằng AH=AK.

b) Gọi I là giao điểm của BH và CK. Chứng minh rằng tia AI là tia phân giác của góc A.

Giải:

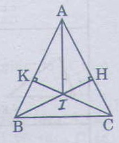
a) Hai tam giác vuông ABH và  ACK có:

AB = AC(gt)

Góc A chung.

nên ∆ABH = ∆ACK(Cạnh huyền- Góc nhọn)

suy ra AH = AK.

b) Hai tam giác vuông AIK và AIH có:

AK = AH(cmt)

AI cạnh chung

Nên ∆AIK = ∆AIH(cạnh huyền- cạnh góc vuông)

Suy ra $\widehat{IAK}$=$\widehat{IAH}$

Vậy AI là tia phân giác của góc A.

Giải:

Ta có: ∆AMD=∆AME(Cạnh huyền AM chung, góc nhọn$\widehat{A_1}$ =  $\widehat{A_2}$)

∆MDB=∆MEC(Cạnh huyền BM=CM, cạnh góc vuông.

MD=ME, do ∆AMD=∆AME)

∆AMB= ∆AMC(Cạnh AM chung),

Cạnh MB=MC, cạnh AB=AC

Vì AD=AE, DB=EC