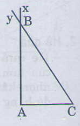
Bài 33 trang 123 - Sách giáo khoa toán 7 tập 1

Vẽ tam giác ABC biết AC=2cm,  

$\hat{A}$= 90⁰ $\hat{C}$ = 60⁰

Giải:

Cách vẽ: 

- Vẽ đoạn AC=2cm,

- Trên cùng một nửa mặt phẳng bờ AC vẽ tia Ax và Cy sao cho $\widehat{CAx}$= 90⁰,

 $\widehat{ACy}$=60⁰ 

Hai tia cắt nhau ở B. tạo thành tam giác ABC cần vẽ. 

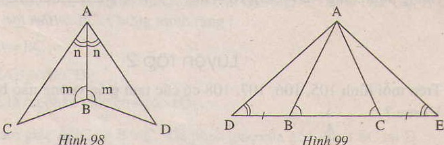
Bài 34 trang 123 - Sách giáo khoa toán 7 tập 1

Trên mỗi hình 98,99 có tam giác nào bằng nhau? Vì sao?

Giải:

Xem hình 98)

∆ABC và ∆ABD có: 

$\widehat{A_1}$=$\widehat{A_2}$(gt)

AB là cạnh chung.

$\widehat{B_1}$=$\widehat{B_2}$(gt)

Nên ∆ABC=∆ABD(g.c.g)

Xem hình 99)

Ta có:

$\widehat{B_1}$+$\widehat{B_2}$=180⁰ (Hai góc kề bù).

$\widehat{C_1}$+ $\widehat{C_2}$=180⁰ (Hai góc kề bù)

Mà $\widehat{B_2}$=$\widehat{C_2}$(gt)

Nên $\widehat{B_1}$=$\widehat{C_1}$

* ∆ABD và ∆ACE có:

$\widehat{B_1}$=$\widehat{C_1}$(cmt)

BD=EC(gt)

$\hat{D}$ = $\hat{E}$(gt)

Nên ∆ABD=∆ACE(g.c.g)

* ∆ADC và ∆AEB có:

$\hat{D}$=$\hat{E}$(gt)

$\widehat{C_2}$=$\widehat{B_2}$(gt)

DC=EB

Nên ∆ADC=∆AEB(g.c.g)

Bài 35 trang 123 - Sách giáo khoa toán 7 tập 1

Cho góc xOy khác góc bẹt, Ot là tia phân giác của góc đó. Qua H thuộc tia Ot , kẻ  đường vuông góc với Ot, nó cắt Ox và Oy  theo thứ tự  A và B.

a) Chứng minh rằng OA=OB.

b ) Lấy điểm C thuộc tia Ot, chứng minh rằng CA=CB và $\widehat{OAC}$= $\widehat{OBC}$.

Giải

a) ∆AOH và  ∆BOH có:$\widehat{AOH}$=$\widehat{BOH}$(gt)

OH là cạnh chung

 ∆AOH =∆BOH( g.c.g)

Vậy OA=OB.

b)  ∆AOC và ∆BOC có:

OA=OB(cmt)

$\widehat{OAC}$=$\widehat{OAB}$(gt)

OC cạnh chung.

Nên  ∆AOC= ∆BOC(g.c.g)

Suy ra: CA=CB(cạnh tương ứng)

$\widehat{OAC}$= $\widehat{OBC}$( góc tương ứng).

Bài 36 trang 123 - Sách giáo khoa toán 7 tập 1

Trên hình 100 ta có OA=OB, OAC=OBD.

Chứng minh rằng AC=BD.

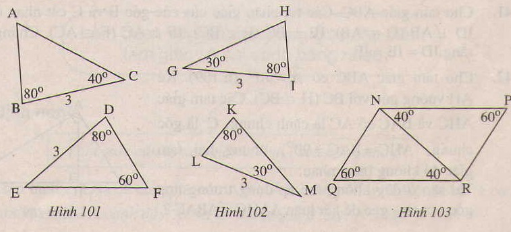
Giải:

Xét ∆OAC  và ∆OBD, có:

$\widehat{OAC}$=$\widehat{OBD}$(gt)

OA=OB(gt)

$\hat{O}$ chung.

Nên ∆OAC=∆OBD(g.c.g)

Suy ra: AC=BD

Bài 37 trang 123 - Sách giáo khoa toán 7 tập 1

Trên mỗi hình 101,102,103 có tam giác nào bằng nhau? Vì sao?

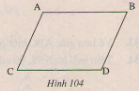
Giải:

Tính các góc còn lại trên mỗi hình trên ta được:

$\hat{A}$=60⁰,$\hat{H}$=70⁰,$\hat{E}$=40⁰

$\hat{L}$=70⁰,$\widehat{RNQ}$=80⁰,$\widehat{RNP}$= 80⁰

Ta được:   ∆ABC và ∆FDE(g. c.g)

Vì $\hat{B}$ = $\hat{D}$

BC=DE

$\hat{C}$=$\hat{E}$

 ∆NQR= ∆RPN(g.c .g)

Vì $\widehat{RNQ}$=$\widehat{RNP}$(=80⁰)

NR là cạnh chung.

$\widehat{NRP}$=$\widehat{RNP}$(40⁰)

Bài 38 trang 124 - Sách giáo khoa toán 7 tập 1

Trên hình 104 ta có AB//CD, AC//BD. Hãy chứng minh rằng 

AB=CD,AC=BD.

Giải.

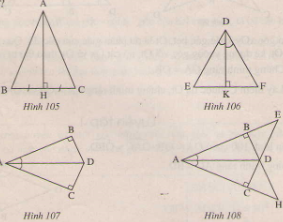
Vẽ đoạn thẳng AD.

∆ADB và ∆DAC có:

 $\widehat{A_1}$= $\widehat{D_1}$(so le trong AB//CD)

AD là cạnh chung.

$\widehat{A_2}$=$\widehat{D_2}$(So le trong, AC//BD)

Do đó ∆ADB=∆DAC(g.c .g)

Suy ra: AB=CD, BD=AC

Bài 39 trang 124 - Sách giáo khoa toán 7 tập 1

Trên mỗi hình 105,106,108 các tam giác vuông nào bằng nhau? Vì sao?

Giải:

Hình 105

∆ABHvà ∆ACH có:

BH=CH(gt)

$\widehat{AHB}$=$\widehat{AHC}$(góc vuông)

AH là cạnh chung.

vậy ∆ABH=∆ACH(g.c.g)

Hình 106

∆DKE và ∆DKF có: 

$\widehat{EDK}$=$\widehat{FDK}$(gt)

DK là cạnh chung.

$\widehat{DKE}$=$\widehat{DKF}$(góc vuông)

Vậy ∆DKE=∆DKF(g.c.g)

Hình 107

Ta có: 

∆ABD=∆ACD(g.c.g)

(Cạnh huyền góc nhọn).

Hình 108

Ta có: 

 ∆ABD=∆ACD(Cạnh huyền - góc nhọn)

∆DBE=∆ACH(g.c.g)

∆ABH=ACE (g.c.g)

Bài 40 trang 124 - Sách giáo khoa toán 7 tập 1

Cho tam giác ABC(AB≠AC), tia Ax đi qua trung điểm M của BC. 

Kẻ BE và CF vuông góc với Ax(E  ∈ Ax, F∈Ax ). So sánh độ dài BE và CF/

Giải

Hai tam giác vuông BME, CMF có:

BM=MC(gt)

$\widehat{BME}$=$\widehat{CMF}$(đối đỉnh)

 Nên ∆BME=∆CMF(cạnh huyền- góc nhọn).

Suy ra BE=CF.

Bài 41 trang 124 - Sách giáo khoa toán 7 tập 1

Cho tam giác ABC, cac tia phân giác của các góc B và C cắt nhau ở I. Vẽ ID 

$\perp$AB(D nằm trên AB), IE $\perp$ BC (E thuộc BC ), IF vuông góc với AC(F thuộc AC)                                   CMR: ID=IE=IF.

Giải:

Hai tam giác vuông BID và BIE có:

BI là cạnh chung

$\widehat{B_1}$=$\widehat{B_2}$(gt)

nên ∆BID=∆BIE.

(cạnh huyền - góc nhọn)

Suy ra ID=IE (1)

Tương tự ∆CIE=CIF(cạnh huyền góc nhọn).

Suy ra: IE =IF (2)

Từ (1)(2) suy ra: ID=IE=IF.

Bài 42 trang 124 - Sách giáo khoa toán 7 tập 1

Cho tam giác ABC có 

$\hat{A}$= 90⁰, kẻ AH vuông góc với BC(H∈BC). C ác tam giác AHC và BAC  có AC là cạnh chung,   là góc chung,  $\widehat{AHC}$=$\widehat{BAC}$=90⁰,

nhưng hai tam giác không bằng nhau. Tại sao ở đây không áp dụng trường hợp góc cạnh góc để kết luận  

∆AHC= ∆BAC?

Giải:

Các tam giác AHC và BAC có:

AC là cạnh chung 

$\hat{C}$ góc chung.

  $\widehat{AHC}$=$\widehat{BAC}$=90⁰,    

Nhưng hai tam giác  không bằng nhau vì góc AHC  không phải là góc kề với AC.

Bài 43 trang 125 - Sách giáo khoa toán 7 tập 1

Cho góc xOy khác góc bẹt. Lấy các điểm A,B thuộc tia Ox sao cho OA<OB.

Lấy các điểm C,D thuộc tia Oy sao cho OC=OA, OD=OB. Gọi E là giao điểm của AD và BC.

Chứng minh rằng:

a) AD=BC;

b) ∆EAB=∆ECD;

c )OE là tia phân giác của xOy.

 Giải:

a) ∆OAD và ∆OCB có: OA= OC(gt)

$\widehat{AOD}$=$\widehat{COB}$(=$\hat{A}$)

OD=OB(gt)

Nên ∆OAD=∆OCB(c.g.c)

suy ra AD=BC.

b) ∆OAD=∆OCB(cmt)

Suy ra: $\hat{D}$= $\hat{B}$

 $\widehat{A_1}$=$\widehat{C_1}$ => $\widehat{A_2}$=$\widehat{C_2}$

Do đó ∆AOE = ∆OCE(c .c.c)

suy ra: $\widehat{OAE}$=$\widehat{COE}$

vậy OE là tia phân giác của xOy.

b) ∆AEB= ∆CED(câu b) => EA=EC.

∆OAE và ∆OCE có: OA=OC(gt)

EA=EC(cmt)

OE là cạnh chung.

Nên ∆OAE=∆(OCE)(c .c.c)

suy ra: $\widehat{AOE}$=$\widehat{COE}$

vậy OE là tia phân giác của góc xOy.

Bài 44 trang 125 - Sách giáo khoa toán 7 tập 1

Cho tam giác ABC có 

$\hat{B}$=$\hat{C}$. Tia phân giác của góc A cắt BC tại D.

Chứng minh rằng.

a)  ∆ADB=∆ADC.

b) AB=AC.

Giải:

a) ∆ADB và ∆ ACD có:

 $\hat{B}$=$\hat{C}$(gt)                                      (1)

$\widehat{A_1}$=$\widehat{A_2}$(AD là tia phân giác)

Nên $\widehat{D_1}$=$\widehat{D_2}$

AD cạnh chung.

Do đó ∆ADB=∆ADC(g.c.g)

b) ∆ADB=∆ADC(câu a)

Suy ra AB=AC .

Bài 45 trang 125 - Sách giáo khoa toán 7 tập 1

Đố:  Cho 4 đoạn thẳng AB,BC,CD,DA trên giấy kẻ ô vuông như ở hinh 110. Hãy lập luận để giải thích:

a) AB=CD, BC=AD;

b) AB//CD.

Giải: 

∆AHB và ∆ CKD có: 

HB=KD.

$\widehat{AHB}$=$\widehat{CKD}$

AH=Ck

Nên ∆ AHB = ∆  CKD(c.g.c)

suy ra AB=CD.

tương tự ∆ CEB = ∆ AFD(c.g.c)

suy ra BC=AD.

b) ∆ABD và ∆CDB  có:

AB=CD(câu a)

BC=AD(câu a)

BD chung.

Do đó ∆ABD=∆CDB(c.c .c)

Suy ra $\widehat{ABD}$=$\widehat{CDB}$

Vậy AB // CD( hai góc so le trong bằng nhau)