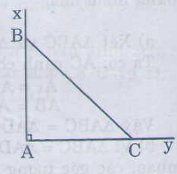Bài 24 trang 118 - Sách giáo khoa toán 7 tập 1

Vẽ tam giác ABC biết 

$\hat{A}$= 90⁰ AB=AC=3cm. Sau đó đo các góc B và C.

Giải:

Cách vẽ:

- Vẽ góc $\widehat{xAy}$=90⁰

- Trên tia Ax vẽ đoạn thẳng AB= 3cm,

- Trên tia Ay vẽ đoạn thẳng AC= 3cm,

- Vẽ đoạn BC.

Ta vẽ được đoạn thẳng BC.

Ta đo các góc B và C ta được $\hat{B}$= $\hat{C}$=45⁰ 

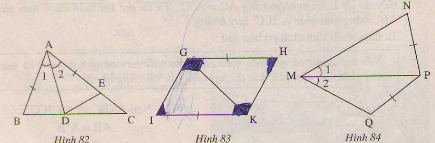
Bài 25 trang 118 - Sách giáo khoa toán 7 tập 1

Trên mỗi hình sau có các tam giác nào bằng nhau? Vì sao?

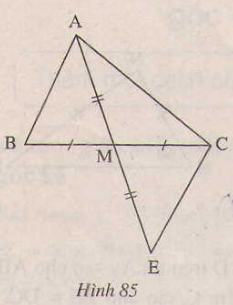
Giải:

Hình 82. 

∆ADB và ∆ADE có: AB=AE(gt)

$\widehat{A_1}$=$\widehat{A_2}$, AD chung.

Nên ∆ADB = ∆ADE(c.g.c)

Hình 83.

∆HGK và ∆IKG có:

HG=IK(gt)

$\hat{G}$=$\hat{K}$(gt)

GK là cạnh chung(gt)

 nên  ∆HGK =  ∆IKG( c.g.c)

Hình 84.  

∆PMQ và ∆PMN có: MP cạnh chung

$\widehat{M_1}$=$\widehat{M_2}$

Nhưng MN không bằng MQ. Nên PMQ không bằng PMN.

Bài 26 trang 118 - Sách giáo khoa toán 7 tập 1

Xét bài toán: 

" Cho tam giác ABC, M là trung điểm của BC, Trên tia đối của MA lấy điểm  E sao cho ME=MA. Chứng minh rẳng AB//CE'.

Dưới đây là hình vẽ và giả thiết, kết luận của bài toán(h.85)

 

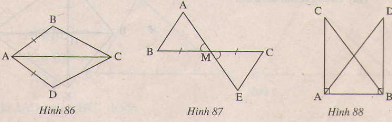
Hãy sắp xếp lại năm câu sau đây một cách hợp lí để giải bài toán  trên:

1) MB = MC(gt)

 $\widehat{AMB}$=$\widehat{EMC}$ (Hai góc đối đỉnh)

MA= ME(Giả thiết)

2) Do đó  ∆AMB=∆EMC(c.g.c)

3)  $\widehat{MAB}$=$\widehat{MEC}$=> AB//CE(hai góc bằng nhau ở vị trí sole trong)

4)  ∆AMB=  ∆EMC => $\widehat{MAB}$=$\widehat{MEC}$ (Hai góc tương ứng)

5)  ∆AMB và  ∆EMC có:

Giải:

Thứ tự sắp xếp là: 5,1,2,4,3

Bài 27 trang 119 - Sách giáo khoa toán 7 tập 1

Nêu thêm một điều kiện để hai tam giác trong mỗi hình vẽ dưới đây là hai tam giác bằng nhau theo trường hợp cạnh-góc- cạnh.

a) ∆ABC= ∆ADC (h.86);

b) ∆AMB= ∆EMC (H.87)

c) ∆CAB= ∆DBA.

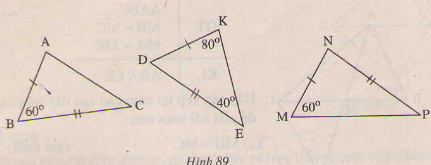
Giải: a) Bổ sung thêm $\widehat{BAC}$=$\widehat{DAC}$.

b) Bổ sung thêm MA=ME

c) Bổ sung thêm AC=BD

Bài 28 trang 120 - Sách giáo khoa toán 7 tập 1

Trên hình 89 có bao nhiêu tam giác bằng nhau.

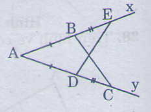
Giải:

Tam giác DKE có: 

$\hat{D}$+$\hat{K}$+$\hat{E}$=90⁰ (tổng ba góc trong của tam giác).

$\hat{D}$+80⁰ +40⁰=180⁰

$\hat{D}$=180⁰ -120⁰= 

Nên 

∆ ABC  và ∆KDE có: 

AB=KD(gt)

$\hat{B}$=$\hat{D}$=60⁰và BE= ED(gt)

Do đó ∆ABC= ∆KDE(c.g.c)

Tam giác MNP không có góc xem giữa hai cạnh tam giác KDE ha ABC nên không bằng hai tam giác còn lại .

Bài 29 trang 120 - Sách giáo khoa toán 7 tập 1

Trên hình 90, các tam giác ABC va A'B'C' có cạnh chung là BC=3cm. 

CA= CA'= 2c m,

$\widehat{ABC}$ =$\widehat{A^{\prime }BC}$ nhưng hai tam giác đó không bằng nhau. 

Tại sao ở đây  không thế áp dùng trường hợp c.g.c để kết luận hai tam giác bằng nhau.

Giải:

Ta có: AC=AD+DC

Hay AC= BA+BE

(do AD=AB, DE=BE)

Nên AC=AE.

∆ABC và ∆ ADE có:

AC=AE(chứng minh trên)

$\hat{A}$ chung

AB=AD(gt)

Vậy ∆ABC =∆ADE(c.g.c)

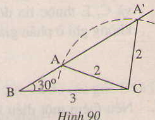
Bài 30 trang 120 - Sách giáo khoa toán 7 tập 1

Trên hình 90, các tam giác ABC và A'BC có cạnh chung BC= 3cm cạnh chung BC = 3cm, CA=CA'= 2cm,

$\widehat{ABC}$=$\widehat{A^{\prime }BC}$= 30⁰nhưng hai tam giác đó không bằng nhau.

Tại sao ở đây không áp dụng trường  hợp cạnh góc cạnh để kết luận ∆ABC=∆A'B 'C'?

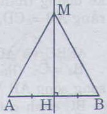
Giải:

Góc ABC không phải là góc xen giữa BC  và CA, Góc A'BC không phải là góc xen giữa hai cạnh BC và CA'. Do đó không thể sử dụng trường hợp cạnh góc cạnh để kết luận ∆ABC=∆A'B 'C' được

Bài 31 trang 120 - Sách giáo khoa toán 7 tập 1

Cho độ dài đoạn thẳng AB, điểm nằm trên đường trung trực của AB, so sánh độ dài các đoạn MA,MB.

Giải: 

Goi H là trung giao điểm của đường trung trực với đoạn AB,∆AHM=∆BHM(c .g.c )

Vậy MA= MB(hai cạnh tương ứng).

 

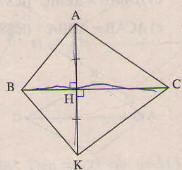
Bài 32 trang 120 - Sách giáo khoa toán 7 tập 1

Tìm các tia phân giác trên hình 91. Hãy chứng minh điều đó.

Giải:

∆AHB và ∆KBH có 

AH=KH(gt)

$\widehat{AHB}$=$\widehat{KHM}$

BH cạnh chung .

nên ∆AHB=∆KBH(c.g.c)

suy ra: $\widehat{ABH}$=$\widehat{KBH}$

Vậy BH là tia phân giác của góc B.

Tương tự     ∆AHC =∆KHC(c.g.c)

Suy ra:  $\widehat{ACH}$=$\widehat{KCH}$

Vậy CH là tia phân giác của góc C