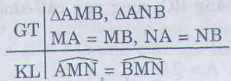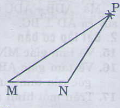
Bài 15 trang 114 - Sách giáo khoa toán 7 tập 1

Vẽ tam giác MNP, biết MN=2,5 cm, NP=3cm, PM= 5cm,

Giải:

-Vẽ đoạn MN= 2,5cm

- Trên cùng một nửa mặt phẳng bở MN vẽ cung trong tâm M bán kính 5cm và cung tròn tâm N bán kinh 5cm.

- Hai cung tròn cắt nhau tại P. Vẽ các đoạn MN, NP, ta được tam giác MNP.

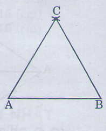
Bài 16 trang 114 - Sách giáo khoa toán 7 tập 1

Vẽ tam giác biết độ dài mỗi cạnh là 3 cm. Sau đó đo góc của mỗi tam  giác.

Giải.

Vẽ tam giác ABC tương tự như hinh vẽ ở bài 15.

Đo mỗi góc của tam giác ABC ta được:

$\hat{A}$=$\hat{B}$=$\hat{C}$= 60⁰

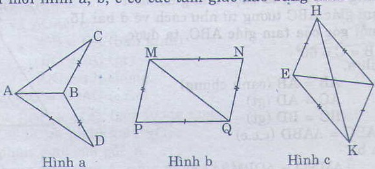
Bài 17 trang 114 - Sách giáo khoa toán 7 tập 1

Trên mỗi hình sau có tam giác nào bằng nhau? Vì sao?

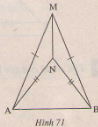
Giải

*  Hình a.

Ta có: AB=AB(cạnh chung)

          AC= AD(gt)

          BC=BD(gt)

vậy ∆ABC= ∆ABD(c.c.c)
* Hình b.

Ta có: 

∆MNQ=∆QPM(c.c.c)

vì MN=QP(gt)

NQ=PM(gt)

MQ=QM(cạnh chung)

* Hình c.

Ta có:

∆EHI=∆IKE(c.c.c) vì

EH=IK(gt)

HI=KE(gt)

EI=IE(gt)

+ ∆EHK=∆IKH(c.c.c) vì

EH=IK(gt)

EK=IH(gt)

HK=KH(cạnh chung)

Bài 18 trang 114 - Sách giáo khoa toán 7 tập 1

Xét bài toán: "

$\Delta$AMB và $\Delta$ANB có MA=MB, NA=NB(h.71). Chứng m inh rằng

$\widehat{AMN}=\widehat{BMN}$."

1) Hãy ghi giả thiết và kết luận của bài toán.

2) Hãy sắp xếp bốn câu sau đây một cách hợp lý để giải bài toán trên :

a) Do đó  $\Delta$AMN=$\Delta$BMN(c.c.c)

b) MN: cạnh chung

MA=MB( Giả thiết)

NA= NB( Giả thiết)

c) Suy ra $\widehat{AMN}=\widehat{BMN}$(2 góc tương ứng)

d)$\Delta$AMB và $\Delta$ANB có:

Giải

1)

                 

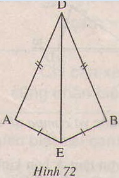
2) sắp xếp theo thư tự.

d,b,a,c.

Bài 19 trang 114 - Sách giáo khoa toán 7 tập 1

Cho hình 72. Chứng minh rằng:

a) ∆ADE = ∆BDE.

b) $\widehat{DAE}=\widehat{DBE}$.

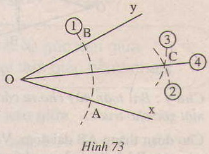
Giải:

Xem hình vẽ:

a) ∆ADE và ∆BDE có

DE cạnh chung

AD=DB(gt)

AE=BE(gt)

Vậy ∆ADE=∆BDE(c.c.c)

b) Từ ∆ADE=∆BDE(cmt)

Suy ra $\widehat{DAE}=\widehat{DBE}$(Hai góc tương ứng)

Bài 20 trang 115 - Sách giáo khoa toán 7 tập 1

Cho góc xOy(h.73), Vẽ cung tròn tâm O, cung tròn này cắt Ox, Oy  theo thứ tự ở A,B (1). Vẽ các cung tròn tâm A và tâm B có cùng bán kính sao cho chúng cắt nhau ở điểm C nằm trong góc xOy ((2) (3)). Nối O với C (4). Chứng minh OC là tia phân giác của góc xOy.

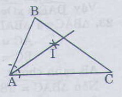
Giải:

xem hình vẽ:

Nối BC, AC.

∆OBC và ∆OAC có:

OB=OA(Bán kính)

BC=AC(gt)

OC  cạnh chung

nên∆OBC = ∆OAC(c.c.c)

Nên $\widehat{BOC}=\widehat{AOC}$(hai góc tương ứng)

Vậy OC là tia phân giác xOy.

Bài 21 trang 115 - Sách giáo khoa toán 7 tập 1

Cho tam giác ABC, Dùng thước và compa, vẽ các tia phân giác của các góc A,B,C.

Giải:

Vẽ tia phân giác của góc A.

Vẽ cung trong tâm A, cung tròn này cắt AB, AC  theo thứ tự ở M,N.

Vẽ các cung tròn tâm M và tâm N có cùng bán kính sao cho chúng cắt nhau ở điểm I nằm trong góc BAC.

Nối AI, ta được AI là tia phân giác của góc A.

Tương tự cho cách vẽ tia phân giác của các góc B,C(Học sinh tự vẽ)

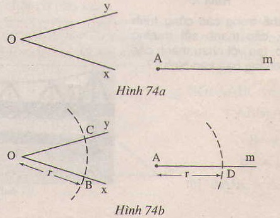
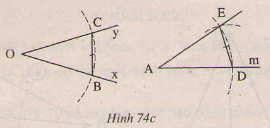
Bài 22 trang 115 - Sách giáo khoa toán 7 tập 1

cho góc xOy và tia Am(h.74a)

Vẽ cung trong tâm O bán kính r, Cung tròn này cắt Ox,Oy theo thứ tự ở B,C

Vẽ cung tròn tâm A bán kính R, cung này cắt kia Am ở D(h.74b).

Vẽ cung tròn tâm D có bán kính bằng BC, cung tròn này cắt cung tròn tam A bán kính r ở E(h. 74c). 

Chứng minh rằng $\widehat{DAE}=\widehat{xOy}.$

 

Giải:

Tam giác DAE và BOC có:

AD=OB(gt)

DE=BC(gt)

AE=OC(gt)

Nên ∆ DAE= ∆ BOC(c.c.c)

suy ra  $\widehat{DAE}$=$\widehat{BOC}$(hai góc tương tứng)

vậy 

$\widehat{DAE}=\widehat{xOy}.$

 

 

$\widehat{DAE}=\widehat{xOy}.$

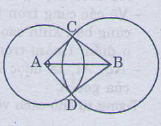
Bài 23 trang 116 - Sách giáo khoa toán 7 tập 1

Cho đoạn thẳng AB dài 4cm Vẽ đường tròn tâm A bán kính 2cm và đường tròn tâm B bán kính 3cm, chúng cắt nhau ở C và D, chứng minh rằng AB là tia phân giác của góc CAD

Giải:

∆BAC và ∆ BAD có: AC=AD(gt)

BC=BD(gt)

AB cạnh chung.

Nên ∆ BAC= ∆ BAD(c.c.c)

Suy ra $\widehat{BAC}$ = $\widehat{BAD}$(góc tương ứng)

Vậy AB là tia phân giác của góc CAD