|
||||||||||||||
|
|
||||||||||||||
|
Tìm kiếm
Danh mục
Hàng mới
 Phần mềm trình chiếu Powerpoint 400.000 VNĐ  Trợ giúp trình chiếu Powerpoint 50.000 VNĐ  Nhận gia công website 999.000 VNĐ
Liên hệ: Minh
0976.775.168
Quảng cáo
|
Bài 44 trang 45 sgk toán 7 - tập 2 Cho hai đa thức: P(x) = -5x3 - + 8x4 + x2 Hãy tính P(x) + Q(x) và P(x) - Q(x). Hướng dẫn giải: Ta có: P(x) = -5x3 - + 8x4 + x2 và Q(x) = x2 – 5x – 2x3 + x4 - . Ta sắp xếp hai đa thức theo lũy thừa giảm dần của biến như sau:
Bài 45 trang 45 sgk toán 7 - tập 2 Cho đa thức P(x) = x4 - 3x2 + – x. Tìm các đa thức Q(x), R(x), sao cho: a) P(x) + Q(x) = x5 – 2x2 + 1. b) P(x) – R(x) = x3. Hướng dẫn giải: Ta có: P(x) = x4 - 3x2 + – x. a) Vì P(x) + Q(x) = x5 – 2x2 + 1 nên Q(x) = x5 – 2x2 + 1 - P(x) Q(x) = x5 – 2x2 + 1 - x4 + 3x2 - + x Q(x) = x5 - x4 + x2 + x + b) Vì P(x) - R(x) = x3 nên R(x) = x4 - 3x2 + – x - x3 hay R(x) = x4 - x3 - 3x2 – x + . Bài 46 trang 45 sgk toán 7 - tập 2 Viết đa thức P(x) = 5x3 – 4x2 + 7x - 2 dưới dạng: a) Tổng của hai đa thức một biến. b) Hiệu của hai đa thức một biến. Bạn Vinh nêu nhận xét: "Ta có thể viết đa thức đã cho thành tổng của hai đa thức bậc 4". Đúng hay sai ? Vì sao ? Hướng dẫn giải: Viết đa thức P(x) = 5x3 – 4x2 + 7x - 2 dưới dạng: a) Tổng của hai đa thức một biến. 5x3 – 4x2 + 7x - 2 = (5x3 – 4x2) + (7x - 2) b) Hiệu của hai đa thức một biến. 5x3 – 4x2 + 7x - 2 = (5x3 + 7x) - (4x2 + 2) Chú ý: Đáp số ở câu a; b không duy nhất, các bạn có thể tìm thêm đa thúc khác. Bạn Vinh nói đúng: Ta có thể viết đa thức đã cho thành tổng của hai đa thúc bậc 4 chẳng hạn như: 5x3 – 4x2 + 7x - 2 = (2x4 + 5x3 + 7x) + (– 2x4 – 4x2 - 2). Bài 47 trang 45 sgk toán 7 - tập 2 Cho các đa thức: P(x) = 2x4 –x - 2x3 + 1 Q(x) = 5x2 – x3 + 4x H(x) = -2x4 + x2 + 5. Tính P(x) + Q(x) + H(x) và P(x) - Q(x) - H(x). Hướng dẫn giải: Ta có: P(x) = 2x4 –x - 2x3 + 1 Q(x) = 5x2 – x3 + 4x H(x) = -2x4 + x2 + 5. Sắp xếp các đa thức theo lũy thừa giảm dần rồi xếp các số hạng đồng dạng theo cùng cột dọc ta được:
Chọn đa thức mà em cho là kết quả đúng: (2x3 - 2x + 1) - (3x2 + 4x - 1) = ?
Hướng dẫn giải: (2x3 - 2x + 1) - (3x2 + 4x - 1) = 2x3 - 3x2 - 6x + 2. Vậy chọn đa thức thứ hai. Bài 49 trang 46 sgk toán 7 - tập 2 Hãy tìm bậc của mỗi đa thức sau:
M = x2 - 2xy + 5x2 - 1 N = x2y2 - y2 + 5x2 - 3x2y + 5. a) Thu gọn các đa thức trên. b) Tính N + M và N - M. Hướng dẫn giải: a) Đa thức M = x2 - 2xy + 5x2 - 1 = 6x2 - 2xy - 1 có bậc 2. Đa thức N = x2y2 - y2 + 5x2 - 3x2y + 5 có bậc 4. b) N + M = x2y2 – y2 + 11x2 – 3x2y + 4 – 2xy N – M = x2y2 – y2 – x2 – 3x2y + 2xy + 6.
Bài 50 trang 46 sgk toán 7 - tập 2 Cho các đa thức: N = 15y3 + 5y2 - y5 - 5y2 - 4y3 - 2y M = y2 + y3 -3y + 1 - y2 + y5 - y3 + 7y5. a) Thu gọn các đa thức trên. b) Tính N + M và N - M. Hướng dẫn giải: a) Thu gọn các đa thức: N = 15y3 + 5y2 - y5 - 5y2 - 4y3 - 2y = -y5 + 11y3 - 2y M = y2 + y3 -3y + 1 - y2 + y5 - y3 + 7y5 = 8y5 - 3y + 1. b) N + M = -y5 + 11y3 - 2y + 8y5 - 3y + 1 = 7y5 + 11y3 - 5y + 1 N - M = -y5 + 11y3 - 2y - 8y5 + 3y - 1= -9y5 + 11y3 + y - 1. Bài 51 trang 46 sgk toán 7 - tập 2 Cho hai đa thức: P(x) = 3x2 - 5 + x4 - 3x3 - x6 - 2x2 - x3; Q(x) = x3 + 2x5 - x4 + x2 - 2x3 + x - 1. a) Sắp xếp các hạng tử của mỗi đa thức theo lũy thừa tăng của biến. b) Tính P(x) + Q(x) và P(x) - Q(x). Hướng dẫn giải: a) Sắp xếp các hạng tử của mỗi đa thức theo lũy thừa tăng của biến. Thu gọn: P(x) = 3x2 - 5 + x4 - 3x3 - x6 - 2x2 - x3 = x2 - 5 + x4 - 4x3 - x6 Sắp xếp: P(x) = -5 + x2 - 4x3 + x4 - x6 Thu gọn: Q(x) = x3 + 2x5 - x4 + x2 - 2x3 + x - 1= -x3 +2x5 - x4 + x2 + x - 1 Sắp xếp: Q(x) = -1 + x + x2 - x3 - x4 + 2x5 b) Ta có:
Bài 52 trang 46 sgk toán 7 - tập 2 Tính giá trị của đa thức P(x) = x2 - 2x - 8 tại: x = -1; x = 0 và x = 4. Hướng dẫn giải: Ta có P(x) = x2 - 2x - 8 => P(-1) = (-1)2 - 2 (-1) - 8 = 1 + 2 - 8 = -5. P(0) = 02 - 2.0 - 8 = -8. P(4) = 42 - 2.4 - 8 = 16 - 8 - 8 = 0. Bài 53 trang 46 sgk toán 7 - tập 2 Cho các đa thức: P(x) = x5 - 2x4 + x2 - x + 1 Q(x) = 6 -2x + 3x3 + x4 - 3x5 . Tính P(x) - Q(x) và Q(x) - P(x). Có nhận xét gì về các hệ số của hai đa thức tìm được ? Hướng dẫn giải:
Nhận xét: Các hệ số tương ứng của hai đa thức tìm được đối nhau. Chú ý: Ta gọi 2 đa thức có các hệ số tương ứng đối nhau là đa thức đối nhau. |
Đăng nhập
Giỏ hàng
Hàng bán chạy
 Phần mềm Quản lý kho Offline 299.000 VNĐ  Monkey Stories 499.000 VNĐ  Monkey Math 499.000 VNĐ
Thống kê
Lượt truy cập : 937455
Số người online : 17 + Khách : 17 + Thành viên : 0
Quảng cáo
|
||||||||||||
| Trang chủGiới thiệuSản phẩmInsight EnglishBHXHDatabaseTiện íchGiải tríKhoảng trờiWall Web | ||||||||||||||
|
||||||||||||||






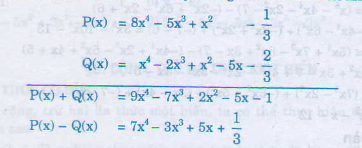
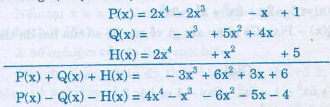 .
.
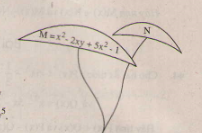
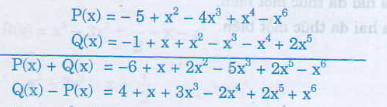 .
.