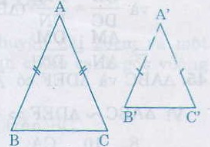
Bài 35 trang 79 - Sách giáo khoa toán 8

Chứng minh rằng nếu tam giác A'B'C' đồng dạng với tam giác ABC theo tỉ số k thì tỉ số của hai đường phân giác tương ứng của chúng cũng bằng K.

Giải:

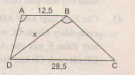
Xét ∆A'B'D' và ∆ABD có:

$\hat{B}$ = $\widehat{B^{\prime }}$ 

$\widehat{BAD}$ = $\widehat{B^{\prime }{A}^{\prime }{D}^{\prime }}$

=> ∆'B'D' ∽ ∆ABD theo tỉ số K = $\frac{A^{\prime }{B}^{\prime }}{AB}$= $\frac{A^{\prime }{D}^{\prime }}{AD}$

Mà  ∆A'B'C' ∽ ∆ABC theo tỉ số = $\frac{A^{\prime }{B}^{\prime }}{AB}$

=> $\frac{A^{\prime }{D}^{\prime }}{AD}$ = k

Bài 36 trang 79 - Sách giáo khoa toán 8

Tính độ dài x của đường thẳng BD trong hình 43(Làm tròn đến chữ thập phân thứ nhất), biết rằng ABCD là hinh thang(AD // CD); AB= 12,5cm; CD= 28,5cm

$\widehat{DAB}$ = $\widehat{DBC}$.

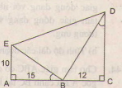
Giải

xét ∆ABD và ∆BDC có:

$\widehat{DBC}$ = $\widehat{DBC}$(gt)

$\widehat{ABD}$ = $\widehat{BDC}$

=> ∆ABD ∽ ∆BDC(trường hợp 3)

=> $\frac{AB}{BD}$ = $\frac{DB}{DC}$ => BD² = AB.DC

=> BD = √(AB.DC) = √(12,5.8,5) => BD = 10,3 cm

Bài 37 trang 79 - Sách giáo khoa toán 8

Hình 44 cho biết 

$\widehat{EBA}$ = $\widehat{BDC}$.

a) Trong hình vẽ, có bao nhiêu tam giác vuông? Hãy kể tên các tam giác đó.

b) Cho biết AE = 10cm, AB = 15cm, BC = 12cn, Hãy tính độ dài các đoạn thẳng CD, BE, BD, ED(làm tròn đén chữ số thập phân thứ nhất).

c) So sánh diện tích tam giác BDE với tổng diện tích hai tam giác AEB và BCD.

Giải: 

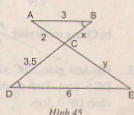
$\widehat{EBA}$ = $\widehat{BDC}$.(gt) mà $\widehat{BCD}$ + $\widehat{CBD}$ = 90⁰ => $\widehat{EBA}$ + $\widehat{CBD}$ = 90⁰

Vậy $\widehat{EBD}$ = 90⁰

Vậy trong hình vẽ có ba tam giác vuông đó là:

∆ABE, ∆CBD, ∆EBD.

b) ∆ABE và ∆CDB có:

 $\hat{A}$ = $\hat{C}$ = 90⁰

$\widehat{ABE}$ = $\widehat{CDB}$ 

=> ∆ABE ∽ ∆CDB => $\frac{AB}{CD}$ = $\frac{AE}{CB}$

=> CD = $\frac{AB.CB}{AE}$ = 18 (cm)

 ∆ABE vuông tại A => BE = $\sqrt{A{E}^2+A{B}^2}$ = $\sqrt{{10}^2+{15}^2}$ = 21,6 (cm).

∆EBD vuông tại B => ED = $\sqrt{E{B}^2+B{D}^2}$ = $\sqrt{325+468}$ = 28.2 (cm)

c) Ta có: $S_{ABE}$ + $S_{DBC}$ = $\frac{1}{2}$AE.AB + $\frac{1}{2}$BC.CD 

= $\frac{1}{2}$. 10.15 + $\frac{1}{2}$12.18

= 75 + 108 = 183 cm²

$S_{ACDE}$= $\frac{1}{2}$(AE + CD).AC

= $\frac{1}{2}$(10 + 18).27= 378 cm²

=> $S_{EBD}$= $S_{EBD}$ - ($S_{ABE}$ + $S_{DBC}$) = 378 - 183 = 195cm²

$S_{EBD}$> $S_{ABE}$ + $S_{DBC}$

Bài 38 trang 79 - Sách giáo khoa toán 8

Tính độ dài x,y của các đoạn thẳng trong hình 45.

Giải:

$\widehat{ABD}$ = $\widehat{BDE}$, lại so le trong

=> AB // DE

=> ∆ABC ∽ ∆EDC

=> $\frac{AB}{ED}$ = $\frac{BC}{DC}$ = $\frac{AC}{EC}$

=> $\frac{3}{6}$ = $\frac{x}{3,5}$ =  $\frac{2}{y}$

=> x = $\frac{3.3,5}{6}$ = 1.75; 

y = $\frac{6.2}{3}$ = 4

Bài 39 trang 79 - Sách giáo khoa toán 8

Cho hình thang ABCD(AB//CD). Gọi O là giao điểm của hai đường chéo AC và BD.

a) Chứng minh rằng OA.OD = OB.OC.

b) Đường thẳng qua O vuông góc với AB và CD theo thứ tự tại H và K.

Chứng minh rằng $\frac{OH}{OK}$ = $\frac{AB}{CD}$

Giải:

a) Vì AB // CD => ∆AOB ∽ ∆COD 

=> $\frac{OA}{OC}$ = $\frac{OB}{OD}$ => OA.OD = OC.OB

b) ∆AOH và ∆COK có:

$\widehat{AHO}$ = $\widehat{CKO}$ = 90⁰

^{$\widehat{HOA}$ = $\widehat{KOC}$}

=>  ∆AOH ∽ ∆COK 

=> $\frac{OH}{OK}$ = $\frac{OA}{OC}$  (1)

mà $\frac{OA}{OC}$ = $\frac{AB}{CD}$  (2)

Từ 1 và 2 => $\frac{OH}{OK}$ = $\frac{AB}{CD}$

Bài 40 trang 80 - Sách giáo khoa toán 8 

Cho tam giác ABC, trong đó AB = 15cm, AC = 20cm, Trên hai cạnh AB và AC lần lượt lấy điểm D và E sao cho AD = 8cm, AE = 6cm. Hai tam giác ABC và ADE có đồng dạng với nhau không? Vì sao?

Giải:

Xét ∆AED và ∆ABC có:

$\frac{AE}{ED}$ = $\frac{6}{8}$ = $\frac{3}{4}$

 

$\frac{AB}{AC}$ = $\frac{15}{20}$ = $\frac{3}{4}$

=> $\frac{AE}{ED}$ = $\frac{AB}{AC}$

Mà $\hat{A}$ chung

=> ∆AED ∽ ∆ABC

Bài 41 trang 80 - Sách giáo khoa toán 8

Tìm dấu hiệu nhận biết hai tam giác cân đồng dạng.

Giải: 

Từ trường hợp 1 ta có:

- Nếu cạnh bên và cạnh dáy của tam giác cân này tỉ lệ với cạnh bên và cạnh đáy của tam giác cân kia thì hai tam giác đó đồng dạng.

Từ trường hợp 2 và 3 ta nói:

- Nếu hai tam giác cân có một góc tương ứng bằng nhau thì hai tam giác đó đồng dạng.

Bài 42 trang 80 - Sách giáo khoa toán 8

So sánh các trường hợp đồng dạng của tam giác với các trường hợp bằng nhau của tam giác (nêu lên những điểm giống nhau  và nhau).

Giải:

Trường hợp	Giống nhau	Khác nhau
		Bằng nhau	Đồng dạng
1	3 cạnh	3 cạnh tương ứng bằng nhau	3 cạnh tương ứng tỉ lệ
2	2 cạnh một góc	Cạnh cạnh tương ứng và một góc kề với hai cạnh bằng nhau	2 cạnh tương ứng tỉ lệ
3		1 cạnh và hai góc kề tương ứng bằng nhau	2 góc tương ứng bằng nhau

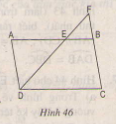
Bài 43 trang 80 - Sách giáo khoa toán 8

Cho hình bình hành ABCD(h46) có độ dài các cạnh AB = 12cm, BC = 7cm. Trên cạnh AB lấy một điểm E sao cho AE = 8cm. Đường thẳng DE cắt CB kéo dài tại F,

a) Trong hình vẽ đã cho có bao nhiêu cặp tam giác đồng dạng? hãy viết các cặp tam giác đồng dạng với nhau theo các đỉnh tương ứng.

b) Tính độ dài đoạn EF và BF, biết rằng DE = 10cm.

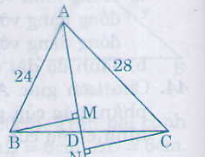
Giải:

a) BE // DC => ∆BEF ∽ ∆CDF

AD // BF => ∆ADE ∽ ∆BFE.

Do đó: ∆ADE ∽ ∆CFD

b) BE = AB - AE = 12 - 8 = 4cm

∆ADE ∽ ∆BFE => $\frac{AE}{BE}$ = $\frac{AD}{BF}$ = $\frac{DE}{EF}$

=> $\frac{8}{4}$ = $\frac{7}{BF}$ = $\frac{10}{EF}$

=> BF = 3,5 cm.

EF = 5 cm.

Bài 44 trang 80 - Sách giáo khoa toán 8

Cho tam giác ABC có các cạnh AB= 24cm, AC = 28cm. Tia phân giác của góc A cắt cạnh BC tại D. Gọi M,N theo thứ tự là hình chiếu của B và C trên AD.

a) Tính tỉ số $\frac{BM}{CN}$

b) Chứng minh rằng $\frac{AM}{AN}$ = $\frac{DM}{DN}$

Giải:

a) AD là đường phân giác của ∆ABC

=> $\frac{DB}{DC}$ = $\frac{AB}{AC}$ = $\frac{DB}{DC}$ = $\frac{24}{28}$ = $\frac{6}{7}$

Mà BM // CN (cùng vuông góc với AD).

=> ∆BMD ∽ ∆CND => $\frac{BM}{CN}$ = $\frac{BD}{CD}$ 

Vậy $\frac{BM}{CN}$ = $\frac{6}{7}$

b) ∆ABM và ∆ACN có: $\widehat{ABM}$ = $\widehat{CAN}$

$\widehat{BMA}$ = $\widehat{CNA}$ = 90⁰

=> ∆ABM ∽ ∆ACN => $\frac{AM}{AN}$ = $\frac{AB}{AC}$.

mà  $\frac{AB}{AC}$ = $\frac{DB}{DC}$ (cmt)

và $\frac{BD}{CD}$ = $\frac{DM}{DN}$

=> $\frac{AM}{AN}$ = $\frac{DM}{DN}$

Bài 45 trang 80 - Sách giáo khoa toán 8

Hai tam giác ABC và DEF có 

$\hat{A}$ = $\hat{D}$, $\hat{B}$ = $\hat{E}$, AB = 8cm, BC = 10cm, DE= 8cm. Tính độ dài các cạnh AC, DF và EF, biết rằng cạnh AC dài hơn cạnh DF là 3cm.

Giải:

∆ABC ∽ ∆DEF vì có $\hat{A}$ = $\hat{D}$, $\hat{B}$ = $\hat{E}$ nên đồng dạng.

Vì ∆ABC ∽ ∆DEF => $\frac{AB}{DE}$ = $\frac{BC}{EF}$ = $\frac{CA}{FD}$

Hay $\frac{8}{6}$ = $\frac{10}{EF}$ = $\frac{CA}{FD}$

Suy ra: EF = 7,5 cm

Vì $\frac{8}{6}$ = $\frac{CA}{FD}$ => $\frac{CA}{8}$ = $\frac{FD}{6}$ = $\frac{CA-FD}{8-6}$ = 3/2

=> CD = $\frac{8.3}{2}$ = 12 cm

FD = 12 -3 = 9cm