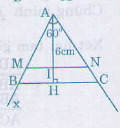
$\widehat{xOy}$=180), Đặt các đoạn thẳng OA= 5cm, OB= 16cm. Trên cạnh thứ hai của góc đó, đặt các đoạn OC= 8cm, OD= 10cm.

a) Chứng minh hai tam giác OCB và OAD đồng dạng.

b) Gọi giao điểm của các cạnh AD và BC là I, chứng minh rằng hai tam giác IAB và ICD có góc các góc bằng nhau từng đôi một.

Giải

a) $\frac{OA}{OC}$ = $\frac{5}{8}$ ; $\frac{OD}{OB}$ = $\frac{10}{16}$ = $\frac{5}{8}$

=> $\frac{OA}{OC}$ = $\frac{OD}{OB}$

Mà O chung nên ∆OCB ∽ ∆OAD( trường hợp 2)

b) ∆ICD và ∆IAI có

 $\widehat{CID}$ = $\widehat{AIB}$ 

$\widehat{CDI}$ = $\widehat{IBA}$

-> $\widehat{CDI}$ = $\widehat{BAI}$

Giải:

Giả sử ∆A'B'C' ∽ ∆ABC theo tỉ số K, AM, A'M' là hai đường trung tuyến tương ứng.

Xét  ∆ABM và ∆A'B'M' có: $\hat{B}$ = $\widehat{B^{\prime }}$(∆A'B'C' ∽ ∆ABC) 

$\frac{A^{\prime }{B}^{\prime }}{AB}$ = $\frac{B^{\prime }{C}^{\prime }}{BC}$ mà B'C' = 2B'M', BC = 2BM

=> ∆A'B'M' ∽ ∆ABM => $\frac{A^{\prime }{M}^{\prime }}{AM}$ = $\frac{A^{\prime }{B}^{\prime }}{AB}$ = k.

$\hat{A}$ = 60⁰ và, tỉ số đường cao $\frac{AB}{AC}$ = $\frac{4}{5}$ và đường cao AH = 6cm.

Giải

Trên hai cạnh Ax, Ay của góc $\widehat{xAy}$ đặt AM = 4 đơn vị, AN = 5 đơn vị. Kẻ đường cao AH của ∆AMN.

Trên tia AI lấy điểm H sao cho AH = 6cm, qua H vẽ đường song song với MN cắt Ax, Ay lần lượt tại B và C => ∆ABC thỏa mãn điều kiện để bài 

Thật vậy:

MN // BC => ∆AMN ∽ ∆ABC => $\frac{AM}{AN}$ = $\frac{AB}{AC}$ = $\frac{4}{5}$

Vậy AH ⊥ BC, AH = 6cm => AH là đường cao.