Bài 15 trang 67 - Sách giáo khoa toán 8

Xem thêm tạiTính x trong hình 24 và làm tròn kết quả đến chữ số thập phân thứ nhất.

Giải:

a) AD là tia phân giác của ∆ABC nên 

 

$\frac{BD}{AB}$ = $\frac{DC}{AC}$ => DC = $\frac{BD.AC}{AB}$ = $\frac{3,5.7,2}{4,5}$

=> x = 5,6

b) PQ là đường phân giác của ∆PMN nên $\frac{MQ}{MP}$ = $\frac{NQ}{NP}$ 

Hay  $\frac{MP}{6,2}$ = $\frac{x}{8,7}$

Áp dụng tính chất của tỉ lệ thức:

=> $\frac{x}{8,7}$ = $\frac{MP}{6,2}$ = $\frac{x+MQ}{8,7+6,2}$ = $\frac{12,5}{14,9}$

=> x≈ 7,3

Bài 16 trang 67 - Sách giáo khoa toán 8

Tam giác ABC có độ dài các cạnh AB= m, AC= n và AD là đường phân giác. Chứng minh rẳng tỉ số diện tích tam giác ABD và diện tích tam giác ACD bằng 

$\frac{m}{n}$.

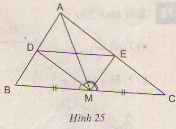
Giải:

Kẻ AH ⊥ BC 

Ta có: 

S_ABD = $\frac{1}{2}$AH.BD

S_ADC  = $\frac{1}{2}$AH.DC

=>$\frac{S_{SBD}}{S_{ADC}}$ = $\frac{\frac{1}{2}AH.BD}{\frac{1}{2}AH.DC}$ = $\frac{BD}{DC}$

Mặt khác: AD là đường phân giác của ∆ABC

=> $\frac{BD}{DC}$= $\frac{AB}{AC}$ = $\frac{m}{n}$.

Vậy $\frac{S_{SBD}}{S_{ADC}}$ = $\frac{m}{n}$

Bài 17 trang 68 - Sách giáo khoa toán 8

Cho tam giác ABC với đường trung tuyến AM. Tia phân giác của góc AMB cắt cạnh AB ở D, tia phân giác của góc AMC cắt cạnh AC ở E. Chứng minh rằng DE // BC(h25)

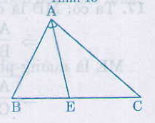
Giải:

Ta có MD là đường phân giác của tam giác ABM

=> $\frac{AD}{BD}$ = $\frac{AM}{BM}$ (1)

ME là đường phân giác của tam giác ACM

=> $\frac{AE}{CE}$ = $\frac{AM}{MC}$ (2)

Mà MB = MC( AM là đường trung tuyến)

=> $\frac{AM}{BM}$ = $\frac{AM}{MC}$ (3)

từ 1,2,3 => $\frac{AD}{BD}$ = $\frac{AE}{CE}$ => DE // BC( Định lí Talet đảo)

Bài 18 trang 68 - Sách giáo khoa toán 8

Tam giác ABC có AB= 5cm, AC= 6cm, BC= 7cm. Tia phân giác của góc BAC cắt BC tại E. Tính các đoạn EB, EC.

Giải:

AE là đường phân giác của tam giác ABC nên 

$\frac{AE}{AB}$ = $\frac{EC}{AC}$ 

Áp dụng tính chất tỉ lệ thức

$\frac{AE}{AB}$ = $\frac{EC}{AC}$ = $\frac{EB+EC}{AB+AC}$= $\frac{BC}{AB+AC}$  

=> EB = $\frac{AB.BC}{AB+AC}$ = $\frac{5.7}{5+6}$

EC = BC- BE ≈ 3,8

Bài 19 trang 68 - Sách giáo khoa toán 8

Cho hình thang ABCD (AB // CD).

Đường thẳng a song song với DC, cắt các cạnh AD và BC theo thứ tự là E và F.

Chứng minh rằng:

a) $\frac{AE}{ED}$ = $\frac{BF}{FC}$;      b) $\frac{AE}{AD}$ = $\frac{BF}{BC}$    c) $\frac{DE}{DA}$ = $\frac{CF}{CB}$.

Giải:

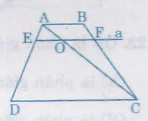
a) Nối AC cắt EF tại O

∆ADC có EO // DC => $\frac{AE}{ED}$ = $\frac{AO}{OC}$       (1)

∆ABC có OF // AB => $\frac{AO}{OC}$ = $\frac{BF}{FC}$         (2)

Từ 1 và 2 => $\frac{AE}{ED}$ = $\frac{BF}{FC}$

b) Từ  $\frac{AE}{ED}$ = $\frac{BF}{FC}$ => $\frac{AE}{ED+AE}$= $\frac{BF}{FC+BF}$

hay  $\frac{AE}{AD}$=$\frac{BF}{BC}$  

c) Từ $\frac{AE}{ED}$ = $\frac{BF}{FC}$  => $\frac{AE+ED}{ED}$= $\frac{BF+FC}{FC}$

=> $\frac{AD}{ED}$ =  $\frac{BF}{FC}$ hay $\frac{ED}{AD}$ = $\frac{FC}{BC}$

Bài 20 trang 68 - Sách giáo khoa toán 8

Cho hình thang ABCD (AB //CD). Hai đường chéo AC và BD cắt nhat tại O. Đường thẳng A qua O và song song với đáy của hình thang cắt các cạnh AD, BC théo thứ tự E và F(h26)

Chứng minh rằng OE = OF.

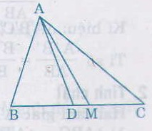
Giải:

∆ADC có OE // OC nên $\frac{OE}{DC}$ = $\frac{AE}{AD}$

∆BDC có OF // DC nên $\frac{OF}{DC}$ = $\frac{BF}{BC}$

Mà AB // CD => $\frac{AE}{AD}$ = $\frac{BF}{BC}$(câu b bài 19)

Vậy $\frac{OE}{DC}$ = $\frac{OF}{DC}$ nên OE = OF.

Bài 21 trang 68 - Sách giáo khoa toán 8

a) Cho tam giác ABC với đường trung tuyến AM và đường phân giác AD. Tính diện tích tam giác ADM, biết AB= m, AC= n( n>m). Và diện tích của tam giác ABC là S.

b) Cho n = 7cm, m = 3cm. Hỏi diện tích tam giác ADM chiếm bao nhiêu phần trăm diện tích tam giác ABC.

Giải:

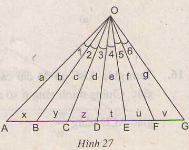
Ta có AD là đường phân giác của ∆ ABC nên

$\frac{S_{ABD}}{S_{ADC}}$ = $\frac{AB}{AC}$ = $\frac{m}{n}$(kết quả ở bài 16)

=> $\frac{S_{ABD}}{S_{ADC}+S_{ABD}}$= $\frac{m}{n+m}$

hay $\frac{S_{ABD}}{S_{ABC}}$= $\frac{m}{n+m}$ => $S_{ABM}$= $\frac{1}{2}$ $S_{ABC}$.

Giả sử AB < AC( m<n) vì AD là đường phân giác, AM là đường trung tuyến kẻ từ A nên AD nằm giữa AB và AM.

=> $S_{ADM}$= $S_{ABM}$ - $S_{ABD}$

=> $S_{ADM}$ = $\frac{1}{2}$S -$\frac{m}{n+m}$S = $\frac{S(m+n-2m)}{2(m+n)}$

$S_{ADM}$= $\frac{S(n-m)}{2(m+n)}$ (với n>m)

Bài 22 trang 68 - Sách giáo khoa toán 8

Đố: Hình 27 cho biết có 6 góc bằng nhau:

$O_1$ = $O_2$ = $O_3$ = $O_4$ = $O_5$ = $O_6$.

Kích thước các đoạn thẳng đã được ghi trên hình. Hãy thiết lập những tỉ lệ thức từ kích thước đã cho.

Giải

OB là tia phân giác trong của ∆OBC => $\frac{x}{a}$ = $\frac{y}{c}$

OC là tia phân giác trong của ∆OBD => $\frac{y}{d}$ = $\frac{z}{d}$

OD là tia phân giác trong của ∆OCE => $\frac{z}{c}$ = $\frac{t}{e}$

OE là tia phân giác trong của ∆ODF => $\frac{t}{d}$ = $\frac{u}{f}$

OC là tia phân giác của  ∆ACE => $\frac{OC}{OA}$ = $\frac{CE}{OE}$ hay $\frac{x+y}{a}$ = $\frac{z+t}{e}$

OE là phân giác của ∆OCG => $\frac{z+t}{c}$ =  $\frac{u+v}{g}$

OD  là phân giác của ∆AOG => $\frac{x+y+x}{a}$ = $\frac{t+u+v}{g}$

OD là phân giác của ∆OBF => $\frac{y+z}{b}$ = $\frac{t+u}{f}$