Bài 1 trang 134 SGK Toán 9 tập 2

Chu vi hình chữ nhật ABCD là 20cm. Hãy tìm giá trị nhỏ nhất của độ dài đường chéo AC.

Hướng dẫn trả lời:

Gọi x (cm) là độ dài cạnh AB (x > 0). Theo đề bài thì độ dài cạnh BC là  (10 – x)

Áp dụng định lí Py-ta-go trong tam giác vuông ABC, ta có:

$\begin{array}{c}A{C}^2=A{B}^2+B{C}^2\\ =x^2+{\left(10-x\right)}^2\\ =2\left(x^2-10x+50\right)\\ =2\left[{\left(x-5\right)}^2+25\right]\\ A{C}^2=2{\left(x-5\right)}^2+50\ge 50\end{array}$ 

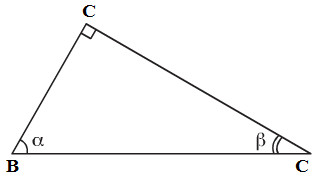
Đẳng thức xảy ra khi : x – 5 = 0 ⇔ x = 5

Vậy giá trị nhỏ nhất của đường chéo AC là √50 = 5√2 (cm)

Bài 2 trang 134 SGK Toán 9 tập 2

Tam giác ABC có góc B = 45^o, góc C = 30^o. Nếu AC = 8 thì AB bằng:

(A) 4               (B) 4√2                        (C) 4√3           (D) 4√6

Hãy chọn câu trả lời đúng.

Hướng dẫn trả lời:

Hạ AH ⊥ BC (H ∈ BC)

Trong tam giác vuông HAC ( $\widehat H = {90^0}$ ) có  . Vậy ∆HAC là nửa tam giác đều cạnh AC, đường cao CH cũng là đường trung tuyến.

$\Rightarrow AH=\frac{AC}{2}=4\left(cm\right)$

Xét hai tam giác vuông HAB ( ) có . Vậy ∆HAB là tam giác vuông cân tại H

⇒ AH = BH = 4 (cm)

Áp dụng định lí Py-ta-go trong tam giác vuông HAB, ta có:

$AB=\sqrt{H{A}^2+H{B}^2}=\sqrt{4^2+4^2}=\sqrt{32}=4\sqrt{2}$ 

Vậy AB = 4√2 cm.

Chọn đáp án B

Bài 3 trang 134 SGK Toán 9 tập 2

Cho tam giác ABC vuông ở C có đường trung tuyến BN vuông góc với đường trung tuyến CM, cạnh BC = a. Tính độ dài đường trung tuyến BN.

Hướng dẫn trả lời:

Gọi G là trọng tâm của tam giác ABC, ta có: $BG=\frac{2}{3}BN$  

Áp dụng hệ thức lượng trong tam giác vuông CNB, ta có:

$\begin{array}{c}B{C}^2=BN.BG=BN.\frac{2}{3}BN=\frac{2}{3}B{N}^2\\ \Rightarrow B{N}^2=\frac{3}{2}B{C}^2=\frac{3a^2}{2}\\ \Rightarrow BN=\sqrt{\frac{3a^2}{2}}=\frac{a\sqrt{3}}{\sqrt{2}}=\frac{a\sqrt{6}}{2}\end{array}$ 

Vậy $BN=\frac{a\sqrt{6}}{2}$

Bài 4 trang 134 SGK Toán 9 tập 2

Nếu tam giác vuông ABC vuông tại C và có 

$\sin A=\frac{2}{3}$ thì tgB bằng:

(A) $\frac{3}{5}$            (B) $\frac{\sqrt{5}}{3}$            (C) $\frac{2}{\sqrt{5}}$         (D) $\frac{\sqrt{5}}{2}$                

Hãy chọn câu trả lời đúng.

Hướng dẫn trả lời:

Trong tam giác vuông ABC $\left(\hat{C}={90}^0\right)$, ta có:

$\sin A=\frac{BC}{AB}=\frac{2}{3}\Rightarrow AB=\frac{3}{2}BC$ 

Áp dụng định lí Py-ta-go trong tam giác vuông ABC, ta có:

$\begin{array}{c}AC=\sqrt{A{B}^2-B{C}^2}=\sqrt{{\left(\frac{3}{2}BC\right)}^2-B{C}^2}\\ AC=\sqrt{\frac{5}{4}B{C}^2}=\frac{BC\sqrt{5}}{2}\end{array}$

Ta có:  $\tan B=\frac{AC}{BC}=\frac{BC\frac{\sqrt{5}}{2}}{BC}=\frac{\sqrt{5}}{2}$

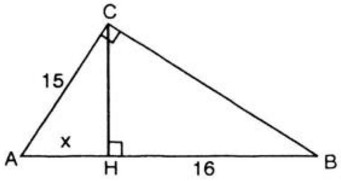
Chọn đáp án D

Bài 5 trang 134 SGK Toán 9 tập 2

Tam giác ABC vuông tại C có AC = 15cm. Đường cao CH chia AB thành hai đoạn AH và HB. Biết HB = 16cm. Tính diện tích tam giác ABC.

Hướng dẫn làm bài:

Đặ AH = x (x > 0)

Áp dụng hệ thức lượng trong tam giác vuông ABC, ta có: AC² = AB.AH

hay 15² = (x + 16)x ⇔ x² + 16x -225 = 0

Giải phương trình, ta được x₁ = 9 (thỏa mãn); x₂ = -25 (loại)

Vậy AH = 9 (cm)

Ta có: HC² = AH. HB = 9. 16 = 144

⇒ HC = 12 (cm)

Vậy diện tích tam gaics ABC là:

$S=\frac{1}{2}AB.CH=\frac{1}{2}.25.12=150\left(c{m}^2\right)$

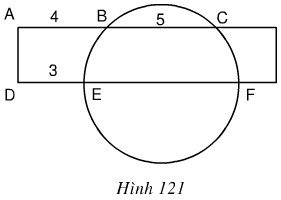
Bài 6 trang 134 SGK Toán 9 tập 2

Một hình chữ nhật cắt đường tròn như hình 121 biết AB = 4, BC = 5, DE = 3 (với cùng đơn vị đo).

Độ dài EF bằng:

(A) 6                (B) 7                (C) $\frac{20}{3}$             (D) 8

Hãy chọn câu trả lời đúng.

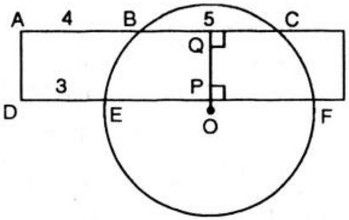
Hướng dẫn làm bài:

Gọi O là tâm của đường tròn. Qua O, kẻ đường vuông góc với BC, cắt DE ở P và BC ở Q.

Ta có:  

$\begin{array}{c}BQ=\frac{1}{2}BC=\frac{5}{2}\\ AQ=AB+BQ=4+\frac{5}{2}=\frac{13}{2}\end{array}$

Vì ADPQ là hình chữ nhật nên AQ = DP

⇒ EP = DP – DE = AQ – DE

hay  $EP=\frac{13}{2}-3=\frac{7}{2}$

Mà $EF=2EP=2.\frac{7}{2}=7$ 

Chọn đáp án B

Bài 7 trang 134 SGK Toán 9 tập 2

Cho tam giác đều ABC, O là trung điểm của BC. Trên các cạnh AB, AC lần lượt lấy các điểm di động D và E sao cho góc DOE = 60^o.

a) Chứng minh tích BD.CE không đổi.

b) Chứng minh ΔBOD ∼ ΔOED. Từ đó suy ra tia DO là tia phân giác của góc BDE.

c) Vẽ đường tròn tâm O tiếp xúc với AB. Chứng minh rằng đường tròn này luôn tiếp xúc với DE.

Hướng dẫn làm bài:

a) Chứng minh tích BD.CE không đổi.

Xét hai tam giác: ∆BOD và ∆CEO, ta có: $\hat{B}=\hat{C}={60}^0$ (gt) (1)

Ta có $\widehat{DOC}$ là góc ngoài của ∆ BDO nên: $\widehat{DOC}=\hat{B}+{\hat{D}}_1$

hay $\widehat{O_1}+\widehat{O_2}=\hat{B}+\widehat{D_1}\iff {60}^0+\widehat{O_2}={60}^0+\widehat{D_1}\iff \widehat{O_2}=\widehat{D_1}\left(2\right)$ 

Từ (1) và (2) ⇒ ∆BOD ~ ∆CEO (g.g)

$\Rightarrow \frac{BD}{BO}=\frac{CO}{CE}\Rightarrow BD.CE=BO.CO$

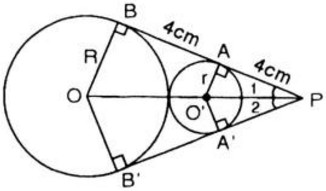
hay $BD.CE=\frac{BC}{2}.\frac{BC}{2}=\frac{B{C}^2}{4}$ (không đổi)

Vậy $BD.CE=\frac{B{C}^2}{4}$ không đổi

b) Chứng minh ΔBOD ∼ ΔOED

Từ câu (a) ta có: ∆BOD ~ ∆CEO

$\Rightarrow \frac{OD}{OE}=\frac{BD}{OC}=\frac{BD}{OB}$ (do OC = OB)

Mà $\hat{B}=\widehat{DOE}={60}^0$ 

Vậy ΔBOD ∼ ΔOED (c.g.c) $\Rightarrow \widehat{BDO}=\widehat{ODE}$  

hay DO là tia phân giác của góc BDE

c) Vẽ OK ⊥ DE và gọi I là tiếp điểm của (O) với AB, khi đó OI ⊥ AB. Xét hai tam giác vuông: IDO và KDO, ta có:

DO: chung

$\widehat{D_1}=\widehat{D_2}$ (chứng minh trên)

Vậy ΔIDO = ΔKDO ⇒ OI = OK

Điều này chứng tỏ rằng OK là bán kính của (O) và OK ⊥ DE nên K là tiếp điểm của DE với (O) hay DE tiếp xúc với đường tròn (O)

Bài 8 trang 134 SGK Toán 9 tập 2

Cho hai đường tròn (O; R) và (O'; r) tiếp xúc ngoài (R > r). Hai tiếp tuyến chung AB và A'B' của hai đường tròn (o),(O') cắt nhau tại P(A và A' thuộc đường tròn (O'), B và B' thuộc đường tròn (O)). Biết PA = AB = 4 cm. Tính diện tích hình tròn (O').

Hướng dẫn làm bài:

Vì AB là tiếp tuyến chung của (O) và  (O’) nên OB ⊥ AB và O’A ⊥ AB

Xét hai tam giác vuông OPB và O’AP, ta có:

$\hat{A}=\hat{B}={90}^0$ 

$\widehat{P_1}$ chung

Vậy ΔOBP ~ ∆ O’AP

$\begin{array}{c}\Rightarrow \frac{r}{R}=\frac{P{O}^{\prime }}{PO}=\frac{PA}{PB}=\frac{4}{8}=\frac{1}{2}\\ \Rightarrow R=2r\end{array}$

Ta có PO’ = OO’ = R + r = 3r (do AO’ là đường trung bình của ∆OBP)

Áp dụng định lí Py-ta-go trong tam giác vuông O’AP

O’P = O’A² + AP² hay (3r)² = r² + 4² ⇔ 9r² = r² + 16 ⇔ 8 r² =16 ⇔ r² = 2

Diện tích đường tròn (O’;r) là: S = π. r² = π.2 = 2π (cm²)

Bài 9 trang 135 SGK Toán 9 tập 2

Cho tam giác ABC nội tiếp đường tròn (O') và ngoại tiếp đường tròn (O). Tia AO cắt đường tròn (O') tại D. Ta có:

(A) CD = BD = O'D ;    (B) AO = CO = OD

(C) CD = CO = BD ;      (D) CD = OD = BD

Hãy chọn câu trả lời đúng.

Hướng dẫn làm bài:

Vì AC vad BC tiếp xúc với đường tròn (O), AD đi qua O nên ta có:

$\widehat{CAD}=\widehat{BAD}=\alpha$ (vì tâm đường tròn nội tiếp trong tam giác là giao điểm của ba đường phân giác trong tam giác)

⇒ cung CD = cung DB ⇒CD = DB (*)

Tương tự, CO là tia phân giác của góc C nên:

$\widehat{ACO}=\widehat{BCO}=\beta$ 

Mặt khác: $\widehat{DCO}=\widehat{DCB}+\widehat{BCO}=\alpha +\beta \left(1\right)(do\widehat{BAD}=\widehat{BCD}$ 

Ta có: $\widehat{COD}$ là góc ngoài của ∆ AOC nên

$\widehat{COD}=\widehat{OAC}+\widehat{OCA}=\beta +\alpha \left(2\right)$ 

Từ (1) và (2) ta có: $\widehat{OCD}=\widehat{COD}$  

Vậy ∆DOC cân tại D (**)

Từ (*) và (**) suy ra CD = OD = BD

Chọn đáp án D

Bài 10 trang 135 SGK Toán 9 tập 2

Cho tam giác nhọn ABC nội tiếp đường tròn(O). Các cung nhỏ AB, BC, CA có số đo lần lượt là x + 75^o, 2x + 25^o, 3x - 22^o. Một góc của tam giác ABC có số đo là:

(A) 57^o5 ;     (B) 59^o ;     (C) 61^o ;     (D) 60^o

Hãy chọn câu trả lời đúng.

Hướng dẫn làm bài:

Vì các cung AB, BC, CA tạo thành đường tròn, do đó:

(x + 75°) + (2x + 25°) + (3x - 22°) = 360°

⇔ 6x + 78° = 360° ⇔ 6x = 282° ⇔ x = 47°

Vậy sđ cung AB = x + 75° =  47° + 75° = 122°

$\Rightarrow \hat{C}=\frac{{122}^0}{2}={61}^0$

sđ cung BC = 2x + 25° = 2.47° + 25° = 119° $\Rightarrow \hat{A}=\frac{{119}^0}{2}=59,5^0$

sđ cung AC = 3x - 22° = 3.47° - 22° = 119° $\Rightarrow \hat{B}=\frac{{119}^0}{2}=59,5^0$  

Chọn đáp án C

Bài 11 trang 135 SGK Toán 9 tập 2

Từ một điểm P ở ngoài đường tròn (O), kẻ cát tuyến PAB và PCD tới đường tròn. Gọi Q là một điểm nằm trên cung nhỏ BD (không chứa A và C) sao cho sđ cung BQ = 42° và sđ cung QD = 38°. Tính tổng 

$\widehat{BPD}+\widehat{AQC}$

Hướng dẫn làm bài:

 Ta có $\widehat{BPD}$ là góc ở ngoài đường tròn (O) nên:

$\widehat{BPD}=\frac{sđcungBQD-sđcungAC}{2}$ 

Ta có $\widehat{AQC}$ là góc nội tiếp trong đường tròn (O) nên:

$\widehat{AQC}=\frac{1}{2}sđcungAC$ 

Do đó:

$\begin{array}{c}\widehat{BPD}+\widehat{AQC}=\frac{sđcungBQF-sđcungAC}{2}+\frac{sđcungAC}{2}\\ =\frac{sđcungBQD}{2}=\frac{{42}^0+{38}^0}{2}={40}^0\end{array}$ 

Vậy $\widehat{BPD}+\widehat{AQC}={40}^0$ 

Bài 12 trang 135 SGK Toán 9 tập 2

Một hình vuông và một hình tròn có chu vi bằng nhau. Hỏi hình nào có diện tích lớn hơn?

Hướng dẫn làm bài:

Giả sử, gọi cạnh hình vuông là a và bán kính đường tròn là R.

Khi đó, chu vi hình vuông là 4a và chu vi hình tròn là 2πR.

Theo đề bài ra ta có: $4a=2\pi R\Rightarrow a=\frac{\pi R}{2}$ 

Ta lập tỉ số diện tích hình vuông và hình tròn:

$\frac{S_{hv}}{S_{htr}}=\frac{a^2}{\pi R^2}=\frac{\left(\frac{\pi R^2}{2}\right)}{\pi R^2}=\frac{{\pi }^2{R}^2}{4\pi R^2}=\frac{\pi }{4}<1$ (vì π ≈ 3,14)

⇒ S_hv < S_htr

Vậy hình tròn có diện tích lớn hơn hình vuông

Bài 13 trang 135 SGK Toán 9 tập 2

Cho đường tròn (O), cung BC có số đo bằng 120^o, điểm A di chuyển trên cung lớn BC. Trên tia đối tia AB lấy điểm D sao cho AD = AC. Hỏi điểm D di chuyển trên đường nào?

Hướng dẫn làm bài:

Ta có  $\hat{A}=\frac{1}{2}sđcungBC={60}^0;\widehat{BDC}=\frac{1}{2}{.60}^0={30}^0$

Như vậy, điểm D tạo với hai mút của đoạn thẳng BC cố định một góc $\widehat{BDC}={30}^0$ nên D chuyển động trên cung chứa góc 30° dựng trên BC.

Ta có, khi A ≡ B thì D ≡ E và khi A ≡ C thì D ≡ C

Vậy khi A di chuyển trên cung lớn BC thì D di chuyển trên cung CE thuộc cung chưa góc 30° dựng trên BC

Bài 14 trang 135 SGK Toán 9 tập 2

Dựng tam giác ABC, biết BC = 4cm, góc A = 60^o, bán kính đường tròn nội tiếp tam giác bằng 1cm.

Hướng dẫn làm bài:

Dựng BC = 4cm và đường thẳng (d) song song với BC và cách BC một khoảng là 1cm

Tâm O của đường tròn nội tiếp ∆ABC là giao điểm của đường thẳng (d) với cung chứa góc 90° + 60° : 2 = 120° dựng trên đoạn BC cố định

Qua B và C vẽ các tiếp tuyến với (O), chúng cắt nhau tại A. Tam giác ABC là tam giác phải dựng

Bài 15 trang 135 SGK Toán 9 tập 2

Tam giác ABC cân tại A có cạnh đáy nhỏ hơn cạnh bên, nội tiếp đường tròn (O).Tiếp tuyến tại B và C của đường tròn lần lượt cắt tia AC và tia AB ở D và E. Chứng minh:

a) BD² = AD.CD

b) Tứ giác BCDE là tứ giác nội tiếp

c) BC song song với DE

Hướng dẫn làm bài:

a) Xét ∆ADB và ∆BDC, ta có:

$\widehat{BAD}=\widehat{CBD}$ (góc nội tiếp cùng chắn cung BC)

$\widehat{D_1}$ góc chung

Vậy ∆ADB ~ ∆BDC ⇒ $\frac{BD}{CD}=\frac{AD}{BD}=B{D}^2=AD.CD$ (đpcm)

b) Ta có $\widehat{AEC}$ là góc có đỉnh ở bên ngoài (O)

 $\widehat{AEC}=\frac{sđcungAC-sđcungBC}{2}=\frac{sđcungAB-sđcungBC}{2}=\widehat{ADB}$

Xét tứ giác BCDE, ta có: $\widehat{AEC}$ và $\widehat{ADB}$ là hai góc liên tiếp cùng nhìn đoạn BC và $\widehat{AEC}=\widehat{ADB}$ . Vậy tứ giác BCDE nội tiếp được trong đường tròn

c) Ta có: $\widehat{ACB}+\widehat{BCD}={180}^0$ 

hay $\widehat{ABC}+\widehat{BCD}={180}^0$ (∆ABC cân tại A)

$\Rightarrow \widehat{ABC}={180}^0-\widehat{BCD}\left(1\right)$ 

Vì BCDE là tứ giác nội tiếp nên

$\widehat{BED}+\widehat{BCD}={180}^0\Rightarrow \widehat{BED}={180}^0-\widehat{BCD}\left(2\right)$ 

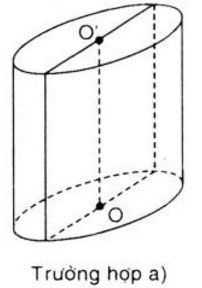
So sánh (1) và (2), ta có: $\widehat{ABC}=\widehat{BED}$ 

Ta cũng có: $\widehat{ABC}$ và $\widehat{BED}$ là hai góc đồng vị. Suy ra: BC // DE (đpcm)

Bài 16 trang 135 SGK Toán 9 tập 2

Một mặt phẳng chứa trụ OO' của một hình trụ; phần mặt phẳng nằm trong hình trụ là một hình chữ nhật có chiều dài 3cm, chiều rộng 2cm.Tính diện tích xung quanh và thể tích hình trụ đó.

Hướng dẫn làm bài:

Bài toán có 2 trường hợp

a)      Đường cao của hình trụ bằng 3cm. Khi đó chiều rộng của hình chữ nhật là đường kính của hình trụ, suy ra R = 1cm

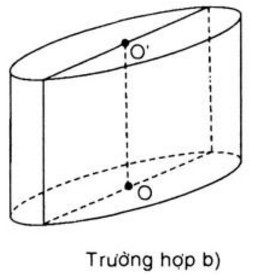
Vậy S_xq = 2πRh = 2π .1 .3 = 6π (cm²)

V = πR²h = π. 1² . 3 = 3π (cm³)

b) Đường cao hình trụ bằng 2cm

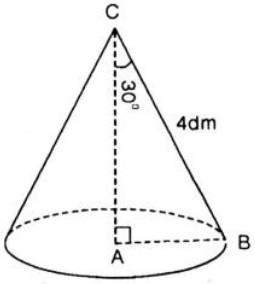
khi đó chiều dài của hình chữ nhật là đường kính của hình trụ, suy ra R = 1,5

Vậy S_xq = 2πRh = 2π . 1,5 . 2 = 6π (cm²)

V = πR²h = π . 1,5² . 2 = 4,5 π (cm²)

Bài 17 trang 135 SGK Toán 9 tập 2

Khi quay tam giác ABC vuông ở A một vòng quanh cạnh góc vuông AC cố định, ta được một hình nón. Biết rằng BC = 4dm, góc ACB = 30^o. Tính diện tích xung quanh và thể tích hình nón.

Hướng dẫn làm bài:

Trong tam giác vuông ABC, ta có:

$\begin{array}{c}AB=BC.\sin C=BC.\sin {30}^0=4.\frac{1}{2}=2\left(dm\right)\\ AC=BC.\cos C=BC.\cos {30}^0=4.\frac{\sqrt{3}}{2}=2\sqrt{3}\left(dm\right)\end{array}$

Ta có: S_xq = πRl = π. 2. 4 = 8 π (dm²)

$V=\frac{1}{3}\pi R^{2}h=\frac{1}{3}\pi {.2}^2.2\sqrt{3}=\frac{8\sqrt{3}.\pi }{3}\left(d{m}^2\right)$

Bài 18 trang 135 SGK Toán 9 tập 2

Một hình cầu có số đo diện tích (đơn vị: m²) bằng số đo thể tích (đơn vị: m³). Tính bán kính hình cầu, diện tích mặt cầu và thể tích hình cầu.

Hướng dẫn làm bài:

Gọi R là bán kính hình cầu (đơn vị : mét)

Khi đó ta có: S = 4πR² và $V=\frac{4}{3}\pi R^3$ 

Theo đề bài ta có: $4\pi R^2=\frac{4}{3}\pi R^3\Rightarrow \frac{R}{3}=1\Rightarrow R=3\left(m\right)$

Ta có: S = 4πR² = 4π . 3² = 36π (m²)

$V=\frac{4}{3}\pi R^3=\frac{4}{3}\pi {.3}^3=36\pi \left(m^3\right)$