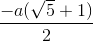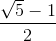|
||||||||||||||
|
|
||||||||||||||
|
Tìm kiếm
Danh mục
Hàng mới
 Phần mềm trình chiếu Powerpoint 400.000 VNĐ  Trợ giúp trình chiếu Powerpoint 50.000 VNĐ  Nhận gia công website 999.000 VNĐ
Liên hệ: Minh
0976.775.168
Quảng cáo
|
Bài 41 trang 58 sgk toán 9Trong lúc học nhóm bạn Hùng yêu cầu bạn Minh và bạn Lan mỗi người chọn một số sao cho hai số này hơn kém nhau là 5 và tích của chúng phải bằng 150. Vậy hai bạn Minh và Lan phải chọn những số nào ? Bài giải.
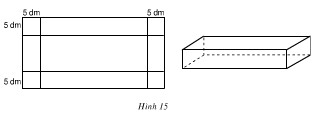
Bài 42 trang 58 sgk toán 9Bác Thời vay 2 000 000 đồng của ngân hàng để làm kinh tế gia đình trong thời hạn một năm. Lẽ ra cuối năm bác phải trả cả vốn lẫn lãi, Song bác đã được ngân hàng cho kéo dài thời hạn thêm một năm nữa, số lãi của năm đầu được gộp vào với vốn để tính lãi năm sau và lãi sất vẫn như cũ. Hết hai năm bác phải trả tất cả là 2 420 000 đồng. Hỏi lãi suất cho vay là bao nhiêu phần trăm trong một năm ? Bài giải: Gọi lãi suất cho vay là x (%), x > 0 Tiền lãi sau một năm là: 2 000 000 . hay 20000x (đồng) Sau 1 năm cả vốn lẫn lãi sẽ là: 2 000 000 + 20000x (đồng) Tiền lãi riêng năm thứ hai phải chịu là: (2 000 000 + 20000x)hay 20000x + 200x2 Số tiền sau hai năm bác Thời phải trả là: 2 000 000 + 40000x + 200x2 Theo đầu bài ra ta có phương trình: 2 000 000 + 40 000x + 200x2 = 2 420 000 hay x2 + 200x - 2 100 = 0 Giải phương trình: ∆' = 1002 - 1 . (-2 100) = 10 000 + 2 100 = 12 100 => √∆' = 110 nên x1 = = -210, x2 = = 10 Vì x > 0 nên x1 không thỏa mãn điều kiện của ẩn. Trả lời: lãi suất là 10%. Bài 43 trang 58 sgk toán 9Một xuồng du lịch đi từ thành phố Cà Mau đến Đất Mũi theo một đường sông dài 120 km. Trên đường đi, xuồng có nghỉ lại 1 giờ ở thị trấn Năm Căn. Khi về, xuồng đi theo đường dài hơn đường lúc đi 5km và vời vận tốc nhỏ hơn vận tốc lúc đi là 5 km/h. Tính vận tốc của xuồng lúc đi, biết rằng thời gian về bằng thời gian đi. Bài giải: Gọi vận tốc của xuồng lúc đi là x (km/h), x > 0, thì vân tốc lúc về là x - 5 (km/h). Vì khi đi có nghỉ 1 giờ nên thời gian khi đi hết tất cả là: + 1 (giờ) Đường về dài: 120 + 5 = 125 (km) Thời gian về là: (giờ) Theo đầu bài có phương trình: + 1 = Giải phương trình: x2 – 5x + 120x – 600 = 125x ⇔ x2 – 10x – 600 = 0 ∆’ = (-5)2 – 1 . (-600) = 625, √∆’ = 25 x1 = 5 – 25 = -20, x2 = 5 + 25 = 30 Vì x > 0 nên x1 = -20 không thỏa mãn điều kiện của ẩn. Trả lời: Vận tốc của xuồng khi đi là 30 km/h Bài 44 trang 58 sgk toán 9Đố em vừa tìm được một số mà một nửa của nó trừ đi một nửa đơn vị rồi nhân với một nửa của nó bằng một đơn vị. Gọi số phải tìm là x. một nửa của nó trừ đi một nửa đơn vị là: - Theo đầu bài ta có phương trình: = hay x2 – x – 2 = 0, có a – b + c = 1 – (-1) – 2 = 0 nên: x1 = -1, x2 = 2 Trả lời: Số phải tìm bằng -1 hoặc 2. Bài 45 trang 59 sgk toán 9Tích của hai số tự nhiên liên tiếp lớn hơn tổng của chúng là 109. Tìm hai số đó. Bài giải: Gọi số bé là x, x ∈ N, x > 0, số tự nhiên kề sau là x + 1. Tích của hai số này là x(x + 1) hay x2 + x. Theo đầu bài ta có phương trình: x2 + x - 2x - 1 = 109 hay x2 - x - 110 = 0 Giải phương trình: ∆ = 1 + 440 = 441, √∆ = 21 x1 = 11, x2 = -10 Vì x > 0 nên x2 = -10 không thỏa mãn điều kiện của ẩn. Trả lời: Hai số phải tìm là: 11 và 12 Bài 46 trang 59 sgk toán 9Một mảnh đất hình chữ nhật có diện tích 240 m2. Nếu tăng chiều rộng 3 m và giảm chiều dài 4 m thì diện tích mảnh đất không đổi. Tính kích thước của mảnh đất. Bài giải: Gọi chiều rộng của mảnh đất là x (m), x > 0. Vì diện tích của mảnh đất bằng 240 m2 nên chiều dài là: (m) Nếu tăng chiều rộng 3m và giảm chiều dài 4m thì mảnh đất mới có chiều rộng là x + 3 (m), chiều dài là ( - 4) (m) và diện tích là: (x + 3)( - 4) ( m2 ) Theo đầu bài ta có phương trình: (x + 3)( - 4) = 240 Giải phương trình: Từ phương trình này suy ra: -4x2 – 12x + 240x + 720 = 240x hay: x2 + 3x – 180 = 0 Giải phương trình: ∆ = 32 + 720 = 729, √∆ = 27 x1 = 12, x2 = -15 Vì x > 0 nên x2 = -15 không thỏa mãn điều kiện của ẩn. Do đó chiều rộng là 12m, chiều dài là: 240 : 12 = 20 (m) Trả lời: Mảnh đất có chiều rộng là 12m, chiều dài là 20m. Bài 47 trang 59 sgk toán 9Bác Hiệp và cô Liên đi xe đạp từ làng lên tỉnh trên quãng đường dài 30 km, khởi hành cùng một lúc. Vận tốc xe của bac Hiệp lớn hơn vận tốc xe của cô Liên là 3 km/h nên bác Hiệp đã đến tỉnh sớm hơn cô Liên nửa giờ. Tính vận tốc xe mỗi người. Bài giải: Gọi vận tốc của bác Hiệp là x (km/h), x > 0 khi đó vận tốc của cố Liên là x - 3 (km/h) Thời gian bác Hiệp đi từ làng lên tỉnh là (giờ). Thời gian bác Liên đi từ làng lên tỉnh là: (giờ) Vì bác Hiệp đến trước cô Liên nửa giờ, tức là thời gian đi của bác Hiệp ít hơn thời gian cô Liên nửa giờ nên ta có phương trình: - = Giải phương trình: x(x - 3) = 60x - 60x + 180 hay x2 – 3x - 180 = 0 x1 = 15, x2 = -12 Vì x > 0 nên x2 = -12 không thỏa mãn điều kiện của ẩn. Vậy: Vận tốc của bác Hiệp là 15 km/h Vận tốc của cô Liên là 12 km/h Bài 48 trang 59 sgk toán 9Từ một miếng tôn hình chữ nhật người ta cắt ở bốn góc bốn hình vuông có cạnh bằng 5 dm để làm thành một cái thùng hình hộp chữ nhật không nắp có dung tích 1500 dm3 (h.15). Hãy tính kích thước của miếng tôn lúc đầu, biết rằng chiều dài của nó gấp đôi chiều rộng.
Bài giải: Gọi chiều rộng của miếng tôn là x (dm), x > 0. Chiều dài của nó là 2x (dm) Khi làm thành một cái thùng không đáy thì chiều dài của thùng là 2x - 10 (dm), chiều rộng là x - 10 (dm), chiều cao là 5 (dm). Dung tích của thùng là 5(2x - 10)(x - 10) (dm3) Theo đầu bài ta có phương trình: 5(2x - 10)(x - 10) = 1500 hay x2 – 15x – 100 = 0 Giải phương trình: ∆ = 225 + 400 = 625, √∆ = 25 x1 = 20, x2 = -5 Đáp số: Miếng tôn có chiều rộng bằng 20 (dm), chiều dài bằng 40 (dm). Bài 49 trang 59 sgk toán 9Hai đội thợ quét sơn một ngôi nhà. Nếu họ cùng làm thì trong 4 ngày xong việc. Nếu họ làm riêng thì đội I hoàn thành công việc nhanh hơn đội II là 6 ngày. Hỏi nếu làm riêng thì mỗi đội phải làm trong bao nhiêu ngày để xong việc ? Bài giải: Gọi thời gian đội I làm một mình xong việc là x (ngày), x > 0. Vì đội II hoàn thành công việc lâu hơn đội I là 6 ngày nên thời gian một mình đội II làm xong việc là x + 6 (ngày). Mỗi ngày đội I làm được (công việc). Mỗi ngày đội II làm được (công việc)
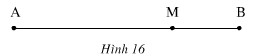
Giải phương trình: x(x + 6) = 4x + 4x + 24 hay x2– 2x - 24 = 0, ∆' = 1 + 24 = 25 = 52 x1 = 1 + 5 = 6, x2 = 1 - 5 = -4 Vì x > 0 nên x2 = -4 không thỏa mãn điều kiện của ẩn. Trả lời: Một mình đội I làm trong 6 ngày thì xong việc. Một mình đội II làm trong 12 ngày thì xong việc. Bài 50 trang 59 sgk toán 9Miếng kim loại thứ nhất nặng 880 g, miếng kim loại thứ hai nặng 858 g. Thể tích của miếng thứ nhất nhỏ hơn thể tích của miếng thứ hai là 10 cm3, nhưng khối lượng riêng của miếng thứ nhất lớn hơn khối lượng riêng của miếng thứ hai là 1 g/cm3 . Tìm khối lượng riêng của mỗi miếng kim loại. Bài giải: Gọi khối lượng riêng của miếng kim loại thứ nhất là: x (g/cm3 ) Khối lượng riêng của miếng kim loại thứ hai là: x - 1 (g/cm3 ) Thể tích của miếng kim loại thứ nhất là: (cm3 ) Thể tích của miếng kim loại thứ hai là: (cm3 ) Theo đầu bài ta có phương trình: - = 10 Giải phương trình: 10x(x - 1) = 858x - 880x + 880 hay 5x2 + 6x - 440 = 0 ∆' =9 + 2200 = 2209, √∆' = 47 x1 = 8,8, x2 = -10 Vì x > 0 nên x2 = -10 (loại) Trả lời: Khối lượng riêng của miếng kim loại thứ nhất là: 8,8 g/cm3 Khối lượng riêng của miếng kim loại thứ hai là: 7,8 g/cm3 Bài 51 trang 59 sgk toán 9Người ta đổ thêm 200 g nước vào một dung dịch chứa 40 g muối thì nồng độ của dung dịch giảm đi 10 %. Hỏi trước khi đổ thêm nước thì dung dịch chứa bao nhiêu nước ? Bài giải: Gọi trọng lượng nước trong dung dịch trước khi đổ thêm nước là: x (g), x > 0 Nồng độ muối của dung dịch khi đó là: Nếu đổ thêm 200 g nước vào dung dịch thì trọng lượng của dung dịch sẽ là: x + 40 + 200 (g) Nồng độ của dung dịch bây giờ là: Vì nồng độ muối giảm 10% nên ta có phương trình: - = Giải phương trình: (x + 40)(x + 240) = 400(x + 240 - x - 40) hay x2 + 280x - 70400 = 0 ∆' = 19600 + 70400 = 90000, √∆' = 300 x1 = 160, x2 = -440 Vì x > 0 nên x2 = -440 (loại) Trả lời: Trước khi đổ thêm nước, trong dung dịch có 160 g nước. Bài 52 trang 60 sgk toán 9Khoảng cách giữa hai bên sông A và B là 30 km. Một canô đi từ bến A đến bến B, nghỉ 40 phút ở bến B rồi quay lại bến A. Kể từ lúc khởi hành đến khi về tời bến A hết tất cả 6 giờ. Hãy tìm vận tốc của canô trong nước yên lặng, biết rằng vận tốc của nước chảy là 3 km/h. Bài giải: Gọi vận tốc thực của canô là x (km/h), x > 3. Gọi vận tốc khi đi xuôi dòng là: x + 3 (km/h) Gọi vận tốc khi ngược dòng là: x - 3 (km/h) Thời gian xuôi dòng là: (giờ) Thời gian ngược dòng là: (giờ) Nghỉ lại 40 phút hay giờ ở B. Theo đầu bài ta có phương trình: + + = 6 Giải phương trình: 16(x + 3)(x - 3) = 90(x + 3 + x - 3) hay: 4x2 - 45x - 36 = 0 ∆ = 2025 + 576 = 2601, √∆ = 51 x1 = 12, x2 = (loại) Trả lời: Vận tốc của canô trong nước yên lặng là 12 km/h. Bài 53 trang 60 sgk toán 9Tỉ số vàng. Đố em chia được đoan AB cho trước thành hai đoạn sao cho tỉ số giữa đoạn lớn với đoạn AB bằng tỉ số giữa đoạn nhỏ với đoạn lớn (h.16). Hãy tìm tỉ số ấy. Đó chính là bài toán mà Ơ-clít đưa ra từ thế kỉ III trước công nguyên. Tỉ số nói trong bài toán được gọi là tỉ số vàng, còn phép chia nói trên được gọi là phép chia vàng hay phép chia hoàng kim.
Hướng dẫn: Giả sử M là điểm chia và AM > MB. Gọi tỉ số cần tìm là x. Bài giải: Giả sử M là điểm chia đoạn AB và AB có độ dài bằng a. Gọi độ dài của AM = x, 0 < x < a. Khi đó MB = a - x. Theo đầu bài: Giải phương trình: x2 = a(a - x) hay x2 + ax - a2 = 0 ∆ = a2 + 4a2 = 5a2 , √∆ = a√5 x1 = Vì x > 0 nên x2 không thỏa mãn điều kiện của ẩn. Vậy AM = Trả lời: Tỉ số cần tìm là: |
Đăng nhập
Giỏ hàng
Hàng bán chạy
 Phần mềm Quản lý kho Offline 299.000 VNĐ  Monkey Stories 499.000 VNĐ  Monkey Math 499.000 VNĐ
Thống kê
Lượt truy cập : 940263
Số người online : 107 + Khách : 107 + Thành viên : 0
Quảng cáo
|
||||||||||||
| Trang chủGiới thiệuSản phẩmInsight EnglishBHXHDatabaseTiện íchGiải tríKhoảng trờiWall Web | ||||||||||||||
|
||||||||||||||







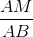 =
= 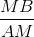 hay
hay 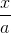 =
= 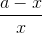
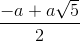 =
= 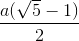 , x2 =
, x2 =