|
||||||||||||||
|
|
||||||||||||||
|
Tìm kiếm
Danh mục
Hàng mới
 Phần mềm trình chiếu Powerpoint 400.000 VNĐ  Trợ giúp trình chiếu Powerpoint 50.000 VNĐ  Nhận gia công website 999.000 VNĐ
Liên hệ: Minh
0976.775.168
Quảng cáo
|
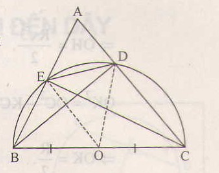
Bài 10 trang 104 sgk toán 9Cho tam giác ABC, các đường cao BD và CE. Chứng minh rằng:a) Bốn điểm B, E, D, C cùng thuộc một đường tròn. b) DE < BC Hướng dẫn giải: a) Gọi O là trung điểm của BC.
Theo tính chất trung tuyến ứng với cạnh huyền ta có:
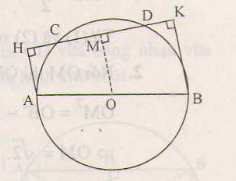
Suy ra Do đó 4 điểm B, C, D, E cùng thuộc đường tròn (O) đường kính BC. b) Xét đường tròn nói ở câu a), BC là đường kính, DE là một dây không qua tâm, do đó DE<BC. Bài 11 trang 104 sgk toán 9Cho đường tròn (O) đường kính AB, dây CD không cắt đường kính AB. Gọi H và K theo thứ tự là chân các đường vuông góc kẻ từ A và B đến CD. Chứng minh rằng CH=DKGợi ý: Kẻ OM vuông góc với CD. Hướng dẫn giải:
Vẽ ta được CM=DM. (1) Ta có OM // AH //BK (cùng vuông góc với CD). Mặt khác , OA=OB nên MH=MK. (2) Từ (1) và (2) suy ra CH=DK. Nhận xét. Kết quả của bài toán trên không thay đổi nếu ta đổi chỗ hai điểm C và D cho nhau. |
Đăng nhập
Giỏ hàng
Hàng bán chạy
 Phần mềm Quản lý kho Offline 299.000 VNĐ  Monkey Stories 499.000 VNĐ  Monkey Math 499.000 VNĐ
Thống kê
Lượt truy cập : 940315
Số người online : 122 + Khách : 122 + Thành viên : 0
Quảng cáo
|
||||||||||||
| Trang chủGiới thiệuSản phẩmInsight EnglishBHXHDatabaseTiện íchGiải tríKhoảng trờiWall Web | ||||||||||||||
|
||||||||||||||