
|
||||||||||||||
|
|
||||||||||||||
|
Tìm kiếm
Danh mục
Hàng mới
 Phần mềm trình chiếu Powerpoint 400.000 VNĐ  Trợ giúp trình chiếu Powerpoint 50.000 VNĐ  Nhận gia công website 999.000 VNĐ
Liên hệ: Minh
0976.775.168
Quảng cáo
|
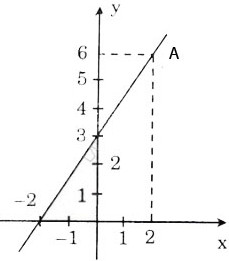
Bài 27 trang 58 sgk toán 9Cho hàm số bậc nhất y = ax + 3. a) Xác định hệ số góc a, biết rằng đồ thị của hàm số đi qua điểm A(2; 6). b) Vẽ đồ thị của hàm số. Bài giải: a) Vì đồ thi của hàm số đi qua điểm A(2; 6) nên ta có 6 = a . 2 + 3. Suy ra hệ số góc a = 1, 5. b) Hàm số đã cho là y = 1,5x + 3. Đồ thị được vẽ như hình bên.
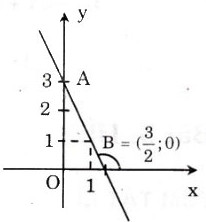
Bài 28 trang 58 sgk toán 9Cho hàm số y = -2x + 3. a) Vẽ đồ thị của hàm số. Bài giải: a) Đồ thị được vẽ như hình bên. b) Gọi α là góc giữa đường thẳng y = -2x + 3 và trục Ox. Thế thì Ta có tg Vậy α ≈ 116034’. Bài 29 trang 59 sgk toán 9Xác định hàm số bậc nhất y = ax + b trong mỗi trường hợp sau: a) a = 2 và đồ thị của hàm số cắt trục hoành tại điểm có hoành độ bằng 1,5. b) a = 3 và đồ thị của hàm số đi qua điểm A(2; 2). c) Đồ thị của hàm số song song với đường thẳng y = √3x và đi qua điểm B(1; √3 + 5). Bài giải: a) Hàm số đã cho là y = 2x + b. Vì đồ thị đi qua điểm A(1,5; 0) nên 0 = 2 . 1,5 + b. Suy ra b = -3. Vậy hàm số đã cho là y = 2x - 3. b) Hàm số đã cho là y = 3x + b. Vì đồ thị đi qua điểm A(2; 2) nên 2 = 3 . 2 + b. Suy ra b = -4. Vậy hàm số đã cho là y = 3x - 4. c) Vì đồ thị của hàm số đã cho song song với đường thẳng y = √3x nên nó có hệ số góc là a = √3. Do đó hàm số đã cho là y = √3x + b. Vì đồ thị đi qua điểm B(1; √3 + 5) nên √3 + 5 = √3 . 1 + b. Suy ra b = 5. Vậy hàm số đã cho là y = √3x + 5. Bài 30 trang 59 sgk toán 9a) Vẽ trên cùng một mặt phẳng tọa độ đồ thị của các hàm số sau: y = b) Gọi giao điểm của hai đường thẳng y = c) Tính chu vi và diện tích của tam giác ABC (đơn vị đo trên các trục tọa độ là xentimét) Bài giải: a) Đồ thị được vẽ như hình bên. b) Giao của đường thẳng y = -x + 2 với Ox là B(2; 0). Vì hai đường thẳng y = 0,5x + 2 và y = -x + 2 đều có tung độ gốc là 2 nên giao của chúng là C(0; 2). Ta có tg A = 0,5. Suy ra Vì ∆BOC là tam giác vuông cân nên Suy ra c) Ta có AB = 6 (cm), AC = Do đó chu vi của ∆ABC là 6 + 2√5 + 2√2 (cm). Diện tích của ∆ABC là: Bài 31 trang 59 sgk toán 9a) Vẽ đồ thị của hàm số y = x + 1; y = 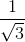 x + √3; y = √3x - √3. x + √3; y = √3x - √3.
b) Gọi α, β, ɣ lần lượt là các góc tạo bởi các đường thẳng trên và trục Ox. Chứng minh rằng tgα = 1, tgβ = Tính số đo các góc α, β, ɣ. Bài giải: a) Đồ thị như hình bên. b) tgα = tgβ = tgɣ = Suy ra α = 450, β = 300, ɣ = 600 . |
Đăng nhập
Giỏ hàng
Hàng bán chạy
 Phần mềm Quản lý kho Offline 299.000 VNĐ  Monkey Stories 499.000 VNĐ  Monkey Math 499.000 VNĐ
Thống kê
Lượt truy cập : 939913
Số người online : 62 + Khách : 62 + Thành viên : 0
Quảng cáo
|
||||||||||||
| Trang chủGiới thiệuSản phẩmInsight EnglishBHXHDatabaseTiện íchGiải tríKhoảng trờiWall Web | ||||||||||||||
|
||||||||||||||






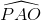 = 1800 - α.
= 1800 - α.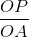 =
= 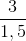 = 2.
= 2. x + 2; y = -x + 2
x + 2; y = -x + 2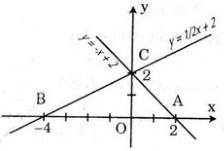
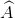 ≈ 26034’.
≈ 26034’.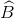 =450 .
=450 .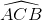 ≈ 1800 – (26034’ + 450) = 108026’.
≈ 1800 – (26034’ + 450) = 108026’.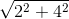 = 2√5 (cm), BC = 2√2 (cm).
= 2√5 (cm), BC = 2√2 (cm).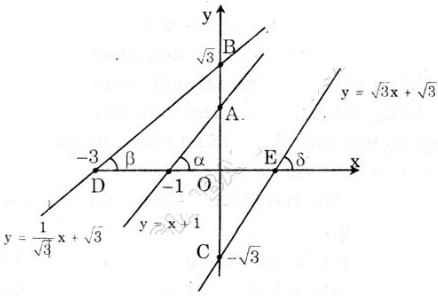
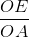 = 1,
= 1,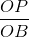 =
= 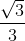 =
= 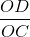 =
= 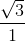 = √3.
= √3.


