|
|||||||||||||||||
|
|
|||||||||||||||||
|
Tìm kiếm
Danh mục
Hàng mới
 Phần mềm trình chiếu Powerpoint 400.000 VNĐ  Trợ giúp trình chiếu Powerpoint 50.000 VNĐ  Nhận gia công website 999.000 VNĐ
Liên hệ: Minh
0976.775.168
Quảng cáo
|
Bài 1 trang 44 sgk toán 9a) Cho hàm số y = f(x) = x. Tính: f(-2); f(-1); f(0); f(); f(1); f(2); f(3). b) Cho hàm số y = g(x) = x + 3. Tính: g(-2); g(-1); g(0); g(); g(1); g(2); g(3). c) Có nhận xét gì về giá trị của hai hàm số đã cho ở trên khi biến x lầy cùng một giá trị ? Bài giải: a) f(-2) = -; f(-1) = -; f(0) = 0; f() = ; f(1) = ; f(2) = ; f(3). = 2. b) g(-2) = ; g(-1) = ; g(0) = 3; g() = ; g(1) = ; g(2) = ; g(3) = 5. c) Khi x lấy cùng một giá trị thì giá trị của g(x) lớn hơn giá trị của f(x) là 3 đơn vị. Bài 2 trang 45 sgk toán 9Cho hàm số y = -  x + 3. x + 3.
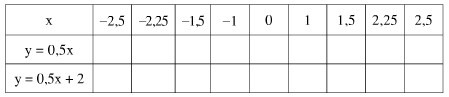
a) Tính các giá trị tương ứng của y theo các giá trị của x rồi điền vào bảng sau:
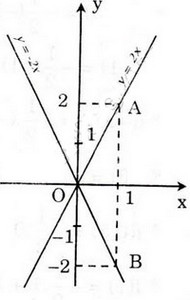
b) Hàm số đã cho là hàm số đồng biến hay nghịch biến ? Vì sao ? Bài giải: a) Với y = -1/2x + 3, ta có f(-2,5) = -1/2(-2,5) + 3 = (2,5 + 6)/2 = 4,25; Tương tự: f(-2) = 4; f(-1,5) = 3,75 ; f(-1) = 3,5 ; f(-0,5) = 3,25; f(0) = 3; f(0,5) = 2,75; f(1) = 2,5 ; f(1,5) = 2,25 ; f(2) = 2 ; f(2,5) = 1,75. b) Hàm số nghịch biến vì khi x tăng lên thì y giảm đi. Bài 3 trang 45 sgk toán 9Cho hai hàm số y = 2x và y = -2x. a) Vẽ trên cùng một mặt phẳng tọa độ đồ thị của hai hàm số đã cho. b) Trong hai hàm số đã cho, hàm số nào đồng biến ? Hàm số nào nghịch biến ? Vì sao ? Bài giải: a) Đồ thị củahàm số y = 2x là đường thẳng đi qua O và điểm A(1; 2). Đồ thị của hàm số y = -2x là đường thẳng đi qua O và điểm B(1; -2). b) Hàm số y = 2x đồng biến vì khi x tăng lên thì y tương ứng tăng lên. Hàm số y = -2x nghịch biến vì khi x tăng lên thì y tương ứng giảm đi.
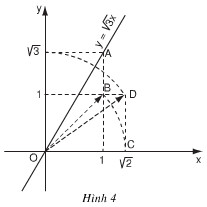
Bài 4 trang 45 sgk toán 9Đồ thị hàm số y = √3 x được vẽ bằng compa và thước thẳng ở hình 4. Hãy tìm hiểu và trình bày lại các bước thực hiện vẽ đồ thị đó.
Bài giải: Ta biết rằng đồ thị hàm số y = √3 x là một đường thẳng đi qua gốc tọa độ. Hơn nữa, khi x = 1 thì y = √3. Do đó điểm A(1; √3) thuộc đồ thị. Vì thế để vẽ đồ thị này, ta phải xác định điểm A trên mặt phẳng tọa độ. Muốn vậy ta phải xác định điểm trên trục tung biểu diễn số √3. Ta có: √3 = Hình vẽ trong SGK thể hiện OC = OB = √2 và theo định lí Py-ta-go OD = Bài 5 trang 45 sgk toán 9a) Vẽ đồ thị hàm số y = x và y =2x trên cùng một mặt phẳng tọa độ Oxy (h.5). b) Đường thẳng song song với trục Ox và cắt trục Oy tại điểm có tung độ Y = 4 lần lượt cắt các đường thẳng y = 2x, y = x tại hai điểm A và B. Tìm tọa độ của các điểm A, B và tính chu vi, diện tích của tam giác OAB theo đơn vị đo trên các trục tọa độ là xentimét.
Bài giải: a) Xem hình trên b) A(2; 4), B(4; 4). Tính chu vi ∆OAB. Dễ thấy AB = 4 - 2 = 2 (cm). Áp dụng định lý Py-ta-go, ta có: OA = Tính diện tích ∆OAB. Gọi C là điểm biểu diễn số 4 trên trục tung, ta có:
= Bài 6 trang 45 sgk toán 9Cho các hàm số y = 0,5x và y = 0,5x + 2 a) Tính giá trị y tương ứng với mỗi hàm số theo giá trị đã cho của biến x rồi điền vào bảng sau:
b) Có nhận xét gì về các giá trị tương ứng của hai hàm số đó khi biến x lấy cùng một giá trị ? Bài giải: a)
b) Khi x lấy cùng một giá trị thì giá trị của hàm số y = 0,5x + 2 lớn hơn giá trị của hàm số y = 0,5x là 2 đơn vị. Bài 7 trang 46 sgk toán 9Cho hàm số y = f(x) = 3x. Cho x hai giá trị bất kì x1, x2 sao cho x1 < x2 . Hãy chứng minh f(x1 ) < f(x2 ) rồi rút ra kết luận hàm số đã cho đồng biến trên R. Bài giải: Từ x1 < x2 và 3 > 0 suy ra 3x1< 3x2 hay f(x1) < f(x2 ). Vậy hàm số đã cho đồng biến trên R. |
Đăng nhập
Giỏ hàng
Hàng bán chạy
 Phần mềm Quản lý kho Offline 299.000 VNĐ  Monkey Stories 499.000 VNĐ  Monkey Math 499.000 VNĐ
Thống kê
Lượt truy cập : 940302
Số người online : 117 + Khách : 117 + Thành viên : 0
Quảng cáo
|
|||||||||||||||
| Trang chủGiới thiệuSản phẩmInsight EnglishBHXHDatabaseTiện íchGiải tríKhoảng trờiWall Web | |||||||||||||||||
|
|||||||||||||||||








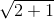 =
= 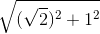 .
.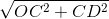 =
= 
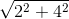 = 2√5 (cm), OB =
= 2√5 (cm), OB = 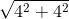 = 4√2 (cm).
= 4√2 (cm).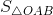 =
= 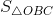 -
- 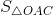 =
=  OC . OB -
OC . OB -