
|
||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||
|
Tìm kiếm
Danh mục
Hàng mới
 Phần mềm trình chiếu Powerpoint 400.000 VNĐ  Trợ giúp trình chiếu Powerpoint 50.000 VNĐ  Nhận gia công website 999.000 VNĐ
Liên hệ: Minh
0976.775.168
Quảng cáo
|
Bài 58 (trang 99 SGK Toán 8 Tập 1):
Lời giải:
Áp dụng định lí Pi-ta-go ta có: - Cột thứ hai: d2 = a2 + b2 = 52 + 122 = 25 + 144 = 169 nên d = 13 - Cột thứ ba: a2 + b2 = d2 => a2 = d2 – b2 = (√10)2 – (√6)2 = 4 nên a = 2 - Cột thứ tư: a2 + b2 = d2 => b2 = d2 – a2 = 72 – (√13)2 = 36 nên b = 6 Bài 59 (trang 99 SGK Toán 8 Tập 1): a) Giao điểm của hai đường chéo của hình chữ nhật là tâm đối xứng của hình chữ nhật đó. b) Hai đường thẳng đi qua trung điểm hai cặp cạnh đối của hình chữ nhật là hai trục đối xứng của hình chữ nhật đó. Lời giải: a) Vì hình bình hành nhận giao điểm của hai đường chéo làm tâm đối xứng, mà hình chữ nhật là một hình bình hành nên giao điểm của hai đường chéo của hình chữ nhật là tâm đối xứng của hình. b) Vì hình thang cân nhận đường thẳng đi qua trung điểm hai đáy làm trục đối xứng, mà hình chữ nhật là một hình thang cân có đáy là hai cạnh đối xứng của hình chữ nhật, do đó hai đường thẳng đi qua trung điểm hai cạnh đối của hình chữ nhật là trục đối xứng của hình. Bài 60 (trang 99 SGK Toán 8 Tập 1): Lời giải: Gọi a là độ dài cạnh huyền của tam giác vuông. Theo định lý Pi-ta-go ta có: a2 = 72 + 242 = 625 => a = 25cm Trung tuyến ứng với cạnh huyền có độ dài bằng nửa độ dài cạnh huyền. Nên trung tuyến ứng với cạnh huyền có đọ dài là 12,5 cm.
Lời giải: 
Ta có: IA = IC (gt) IE = IH (gt) Nên AHCE là hình bình hành (dấu hiệu nhận biết 4) Ta lại có góc ∠AHC = 1v Nên AHCE là hình chữ nhật (dấu hiệu nhận biết 3) (Hoặc hình bình hành AHCE là hình chữ nhật vì có hai đường chéo bằng nhau). Bài 62 (trang 99 SGK Toán 8 Tập 1): a) Nếu tam giác ABC vuông tại C thì điểm C thuộc đường tròn có đường kính là AB (h.88) b) Nếu điểm C thuộc đường tròn có đường kính là AB (C khác A và B) thì tam giác ABC vuông tại C (h.89). 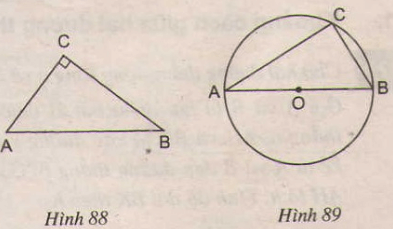 Lời giải: Lời giải:
a) Đúng Gọi O là trung điểm của AB. Ta có CO là trung tuyến ứng với cạnh huyền nên 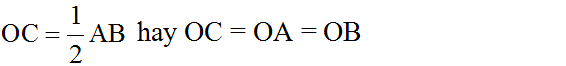
Nên A, B, C cùng thuộc đường tròn bán kính OA. Vậy C thuộc đường tròn đường kính AB. b) Đúng Gọi O là tâm đường tròn. Tam giác ABC có trung tuyến CO bằng nửa cạnh AB (do CO = AO = OB) nên tam giác ABC vuông tại C. Bài 63 (trang 100 SGK Toán 8 Tập 1): 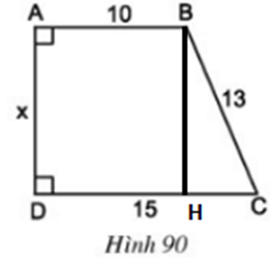
Lời giải: Kẻ BH ⊥ CD Suy ra DH = 10 nên HC = 5 Do đó BH2 = 132 – 52 = 169 – 25 = 144 => BH = 12 Vậy x = 12 Bài 64 (trang 100 SGK Toán 8 Tập 1): 
Lời giải: ΔDEC có: 
Tứ giác EFGH có ba góc vuông nên là hình chữ nhật. Bài 65 (trang 100 SGK Toán 8 Tập 1): Lời giải: 
Ta có EB = EA, FB = FC (gt) Nên EF là đường trung bình của ΔABC Do đó EF // AC HD = HA, GD = GC nên HG là đường trung bình của ΔADC Do đó HG // AC suy ra EF // HG. Tương tự EH // FG Do đó EFGH là hình bình hành. EF // AC và BD ⊥ AC nên BD ⊥ EF 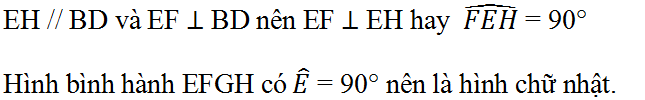
Bài 66 (trang 100 SGK Toán 8 Tập 1): Lời giải: 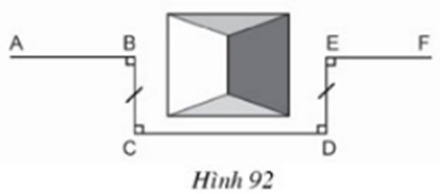
Tứ giác BCDE có: BC // DE (vì cùng vuông góc với CD); BC = DE nên BCDE là hình bình hành 
Suy ra AB và EF cùng nằm trên một đường thẳng.
|
Đăng nhập
Giỏ hàng
Hàng bán chạy
 Phần mềm Quản lý kho Offline 299.000 VNĐ  Monkey Stories 499.000 VNĐ  Monkey Math 499.000 VNĐ
Thống kê
Lượt truy cập : 937515
Số người online : 48 + Khách : 48 + Thành viên : 0
Quảng cáo
|
||||||||||||||||||||||||
| Trang chủGiới thiệuSản phẩmInsight EnglishBHXHDatabaseTiện íchGiải tríKhoảng trờiWall Web | ||||||||||||||||||||||||||
|
||||||||||||||||||||||||||









