Bài 43 (trang 92 SGK Toán 8 Tập 1): 
Các tứ giác ABCD, EFGH, MNPQ trên giấy kẻ ô vuông ở hình 71 có là hình bình hành hay không?

Lời giải:

Cả ba tứ giác là hình bình hành

- Tứ giác ABCD là hình bình hành vì có AB // CD và AB = CD = 3 (dấu hiệu nhận biết 3)

- Tứ giác EFGH là hình bình hành vì có EH // FG và EH = FH = 3 (dấu hiệu nhận biết 3)

- Tứ giác MNPQ là hình bình hành vì có MN = PQ và MQ = NP (dấu hiệu nhận biết 2)

(Chú ý:

- Với các tứ giác ABCD, EFGH còn có thể nhận biết là hình bình hành bằng dấu hiệu nhận biết 2.

- Với tứ giác MNPQ còn có thể nhận biết là hình bình hành bằng dấu hiệu nhận biết 5.)

Bài 44 (trang 92 SGK Toán 8 Tập 1): 
Cho hình bình hành ABCD. Gọi E là trung điểm của AD, F là trung điểm của BC. Chứng minh rằng BE = DF

Lời giải:

Ta có:

Mà AD = BF (ABCD là hình bình hành)

=> DE = BF

Tứ giác BEDF có:

    DE // BF (vì AD // BC)

    DE = BF

Nên BEDF là hình bình hành suy ra BE = DF

Bài 45 (trang 92 SGK Toán 8 Tập 1): 
Cho hình bình hành ABCD (AB > BC). Tia phân giác của góc D cắt AB ở E, tia phân giác của góc B cắt CD ở F.

a) Chứng minh rằng DE // BF

b) Tứ giác DEBF là hình gì? Vì sao?

Lời giải:

a) Ta có:

Do đó DE // BF (có hai góc đồng vị bằng nhau)

b) Tứ giác DEBF có:

    DE // BF (chứng minh ở câu a)

    BE // DF (vì AB // CD)

Nên theo định nghĩa DEBF là hình bình hành.

Bài 46 (trang 92 SGK Toán 8 Tập 1): 
Các câu sau đúng hay sai?

a) Hình thang có hai cạnh đáy bằng nhau là hình bình hành

b) Hình thang có hai cạnh bên song song là hình bình hành

c) Tứ giác có hai cạnh đối bằng nhau là hình bình hành

d) Hình thang có hai cạnh bên bằng nhau là hình bình hành

Lời giải:

a) Đúng, vì hình thang có hai đáy song song lại có thêm hai cạnh đáy bằng nhau nên là hình bình hành theo dấu hiệu nhận biết 5

b) Đúng, vì khi đó ta được tứ giác có các cạnh đối song song là hình bình hành (định nghĩa)

c) Sai, vì hình thang cân có hai cạnh đối (hai cạnh bên) bằng nhau nhưng nó không phải là hình bình hành

d) Sai, vì hình thang cân có hai cạnh bên bằng nhau nhưng nó không phải là hình bình hành.

Bài 47 (trang 93 SGK Toán 8 Tập 1): 
Cho hình 72. Trong đó ABCD là hình bình hành

a) Chứng minh rằng AHCK là hình bình hành

b) Gọi O là trung điểm của HK. Chứng minh rằng ba điểm A, O, C thẳng hàng.

Lời giải:

a) ABCD là hình bình hành

=> AB // CD

Nên ΔAHD = ΔCKB (cạnh huyền, góc nhọn) => AH = CK

Lại có AH ⊥ BD; CK ⊥ BD => AH // CK

Tứ giác AHCK có AH // CK, AH = CK nên là hình bình hành.

b) Xét hình bình hành AHCK, trung điểm O của đường chéo HK cũng là trung điểm của đường chéo AC (tính chất đường chéo của hình bình hành). Do đó ba điểm A, O, C thẳng hàng

Bài 48 (trang 93 SGK Toán 8 Tập 1): 
Tứ giác ABCD có E, F , G, H theo thứ tự là trung điểm của các cạnh AB, BC, CD, DA. Tứ giác EFGH là hình gì? Vì sao?

Lời giải:

Tứ giác EFGH là hình bình hành

- Cách 1:

EB = EA, FB = FC (gt) nên EF là đường trung bình của ΔABC

Do đó EF // AC.

Tương tự HG là đường trung bình của ΔACD do đó HG // AC

Suy ra EF // HG         (1)

Tương tự: EH // FG         (2)

Từ (1) và (2) suy ra EFGH là hình bình hành (dấu hiệu nhận biết 1).

- Cách 2:

Suy ra EF = HG.

Lại có EF // HG (cmt)

Vậy EFGH là hình bình hành (dấu hiệu nhận biết 3)

Bài 49 (trang 93 SGK Toán 8 Tập 1): 
Cho hình bình hành ABCD. Gọi I, K theo thứ tự là trung điểm của CD, AB. Đường chéo BD cắt AI, CK theo thứ tự ở M và N. Chứng minh rằng:

a) AI // CK

b) DM = MN = NB

Lời giải: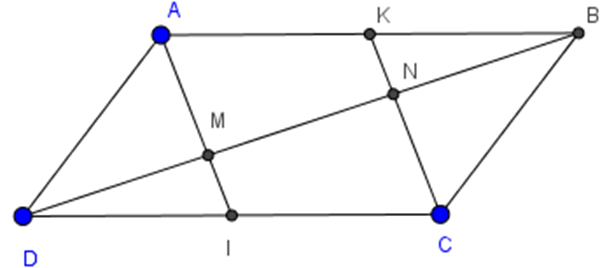

a)

Mà AB = CD (ABCD là hình bình hành).

=> AK = IC

Tứ giác AKCI có AK = CI, AK// CI nên AKCI là hình bình hành.

Do đó AI // CK

b) ΔDCN có DI = IC, IM // MN (vì AI // CK) nên suy ra DM = MN

Chứng minh tương tự đối với ΔABM ta có MN = NB.

Vậy DM = MN = NB (đpcm).